Instruction Set Architecture

Triton VM is a stack machine with RAM. It is a Harvard architecture with read-only memory for the program. The arithmetization of the VM is defined over the B-field ${\mathbb{F}}_p$ where $p$ is the Oxfoi prime, i.e., $2^{64}-2^{32}+1$.¹ This means the registers and memory elements take values from ${\mathbb{F}}_p$, and the transition function gives rise to low-degree transition verification polynomials from the ring of multivariate polynomials over ${\mathbb{F}}_p$.

Instructions have variable width: they either consist of one word, i.e., one B-field element, or of two words, i.e., two B-field elements. An example for a single-word instruction is pop, removing the top of the stack. An example for a double-word instruction is push + arg, pushing arg to the stack.

Triton VM has two interfaces for data input, one for public and one for secret data, and one interface for data output, whose data is always public. The public interfaces differ from the private one, especially regarding their arithmetization.

Data Structures

Memory

The term memory refers to a data structure that gives read access (and possibly write access, too) to elements indicated by an address. Regardless of the data structure, the address lives in the B-field. There are four separate notions of memory:

1. RAM, to which the VM can read and write field elements.
2. Program Memory, from which the VM reads instructions.
3. OpStack Memory, which stores the operational stack.
4. Jump Stack Memory, which stores the entire jump stack.

Operational Stack

The stack is a last-in;first-out data structure that allows the program to store intermediate variables, pass arguments, and keep pointers to objects held in RAM. In this document, the operational stack is either referred to as just “stack” or, if more clarity is desired, “OpStack.”

From the Virtual Machine's point of view, the stack is a single, continuous object. The first 16 elements of the stack can be accessed very conveniently. Elements deeper in the stack require removing some of the higher elements, possibly after storing them in RAM.

For reasons of arithmetization, the stack is actually split into two distinct parts:

1. the operational stack registers st0 through st15, and
2. the OpStack Underflow Memory.

The motivation and the interplay between the two parts is described and exemplified in arithmetization of the OpStack table.

Random Access Memory

Triton VM has dedicated Random Access Memory. It can hold up to $p$ many base field elements, where $p$ is the Oxfoi prime¹. Programs can read from and write to RAM using instructions read_mem and write_mem.

The initial RAM is determined by the entity running Triton VM. Populating RAM this way can be beneficial for a program's execution and proving time, especially if substantial amounts of data from the input streams needs to be persisted in RAM. This initialization is one form of secret input, and one of two mechanisms that make Triton VM a non-deterministic virtual machine. The other mechanism is dedicated instructions.

Jump Stack

Another last-in;first-out data structure that keeps track of return and destination addresses. This stack changes only when control follows a call or return instruction.

Registers

This section covers all columns in the Processor Table. Only a subset of these registers relate to the instruction set; the remaining registers exist only to enable an efficient arithmetization and are marked with an asterisk (*).

Instruction

Register ip, the instruction pointer, contains the address of the current instruction in Program Memory. The instruction is contained in the register current instruction, or ci. Register next instruction (or argument), or nia, either contains the next instruction or the argument for the current instruction in ci. For reasons of arithmetization, ci is decomposed, giving rise to the instruction bit registers, labeled ib0 through ib7.

Stack

The stack is represented by 16 registers called stack registers (st0 – st15) plus the OpStack Underflow Memory. The top 16 elements of the OpStack are directly accessible, the remainder of the OpStack, i.e, the part held in OpStack Underflow Memory, is not. In order to access elements of the OpStack held in OpStack Underflow Memory, the stack has to shrink by discarding elements from the top – potentially after writing them to RAM – thus moving lower elements into the stack registers.

The stack grows upwards, in line with the metaphor that justifies the name "stack".

For reasons of arithmetization, the stack always contains a minimum of 16 elements. All these elements are initially 0. Trying to run an instruction which would result in a stack of smaller total length than 16 crashes the VM.

The registers osp and osv are not directly accessible by the program running in TritonVM. They exist only to allow efficient arithmetization.

RAM

The registers ramp and ramv are not directly accessible by the program running in TritonVM. They exist only to allow efficient arithmetization.

Helper Variables

Some instructions require helper variables in order to generate an efficient arithmetization. To this end, there are 7 helper variable registers, labeled hv0 through hv6. These registers are part of the arithmetization of the architecture, but not needed to define the instruction set.

Because they are only needed for some instructions, the helper variables are not generally defined. For instruction group stack_shrinks_and_top_3_unconstrained and its derivatives, as well as for instructions dup, swap, skiz, divine_sibling, split, and eq, the behavior is defined in the respective sections.

Instructions

Most instructions are contained within a single, parameterless machine word.

Some instructions take a machine word as argument and are so considered double-word instructions. They are recognized by the form “instr + arg”.

Regarding Opcodes

An instruction's operation code, or opcode, is the machine word uniquely identifying the instruction. For reasons of efficient arithmetization, certain properties of the instruction are encoded in the opcode. Concretely, interpreting the field element in standard representation:

• for all double-word instructions, the least significant bit is 1.
• for all instructions shrinking the operational stack, the second-to-least significant bit is 1.
• for all u32 instructions , the third-to-least significant bit is 1.

The first property is used by instruction skiz. The second property helps guarantee that operational stack underflow cannot happen. It is used by several instructions through instruction group stack_shrinks_and_top_3_unconstrained. The third property allows efficient arithmetization of the running product for the Permutation Argument between Processor Table and U32 Table.

OpStack Manipulation

Instruction divine (together with divine_sibling) make TritonVM a virtual machine that can execute non-deterministic programs. As programs go, this concept is somewhat unusual and benefits from additional explanation. The name of the instruction is the verb (not the adjective) meaning “to discover by intuition or insight.”

From the perspective of the program, the instruction divine makes some element a magically appear on the stack. It is not at all specified what a is, but generally speaking, a has to be exactly correct, else execution fails. Hence, from the perspective of the program, it just non-deterministically guesses the correct value of a in a moment of divine clarity.

Looking at the entire system, consisting of the VM, the program, and all inputs – both public and secret – execution is deterministic: the value a was supplied as a secret input.

Control Flow

Memory Access

Hashing

The instruction hash works as follows. The stack's 10 top-most elements (jihgfedcba) are reversed and concatenated with six zeros, resulting in abcdefghij000000. The permutation xlix is applied to abcdefghij000000, resulting in αβγδεζηθικuvwxyz. The first five elements of this result, i.e., αβγδε, are reversed and written to the stack, overwriting st5 through st9. The top elements of the stack st0 through st4 are set to zero. For example, the old stack was _ jihgfedcba and the new stack is _ εδγβα 00000.

The instruction divine_sibling works as follows. The 11th element of the stack i is taken as the node index for a Merkle tree that is claimed to include data whose digest is the content of stack registers st5 through st9, i.e., edcba. The sibling digest of edcba is zyxwv and is read from the input interface of secret data. The least-significant bit of i indicates whether edcba is the digest of a left leaf or a right leaf of the Merkle tree's base level. Depending on this least significant bit of i, divine_sibling either

1. (i = 0 mod 2, i.e., current node is left sibling) moves edcba into registers st0 through st4 and moves zyxwv into registers st5 through st9, or
2. (i = 1 mod 2, i.e., current node is right sibling) does not change registers st5 through st9 and moves zyxwv into registers st0 through st4.

The 11th element of the operational stack i is shifted by 1 bit to the right, i.e., the least-significant bit is dropped. In conjunction with instruction hash and assert_vector, the instruction divine_sibling allows to efficiently verify a Merkle authentication path.

The instructions absorb_init, absorb, and squeeze are the interface for using the permutation xlix in a Sponge construction. The capacity is never accessible to the program that's being executed by Triton VM. At any given time, at most one Sponge state exists. Only instruction absorb_init resets the state of the Sponge, and only the three Sponge instructions influence the Sponge's state. Notably, executing instruction hash does not modify the Sponge's state. When using the Sponge instructions, it is the programmer's responsibility to take care of proper input padding: Triton VM cannot know the number of elements that will be absorbed.

Base Field Arithmetic on Stack

Bitwise Arithmetic on Stack

Extension Field Arithmetic on Stack

Input/Output

Arithmetization

An arithmetization defines two things:

1. algebraic execution tables (AETs), and
2. arithmetic intermediate representation (AIR) constraints.

For Triton VM, the execution trace is spread over multiple tables. These tables are linked by various cryptographic arguments. This division allows for a separation of concerns. For example, the main processor's trace is recorded in the Processor Table. The main processor can delegate the execution of somewhat-difficult-to-arithmetize instructions like hash or xor to a co-processor. The arithmetization of the co-processor is largely independent from the main processor and recorded in its separate trace. For example, instructions relating to hashing are executed by the hash co-processor. Its trace is recorded in the Hash Table. Similarly, bitwise instructions are executed by the u32 co-processor, and the corresponding trace recorded in the U32 Table. Another example for the separation of concerns is memory consistency, the bulk of which is delegated to the Operational Stack Table, RAM Table, and Jump Stack Table.

Algebraic Execution Tables

There are 9 Arithmetic Execution Tables in TritonVM. Their relation is described by below figure. A a blue arrow indicates a Permutation Argument, a red arrow indicates an Evaluation Argument, a purple arrow indicates a Lookup Argument, and the green arrow is the Contiguity Argument.

The grayed-out elements “program digest”, “input”, and “output” are not AETs but publicly available information. Together, they constitute the claim for which Triton VM produces a proof. See “Arguments Using Public Information” and “Program Attestation” for the Evaluation Arguments with which they are linked into the rest of the proof system.

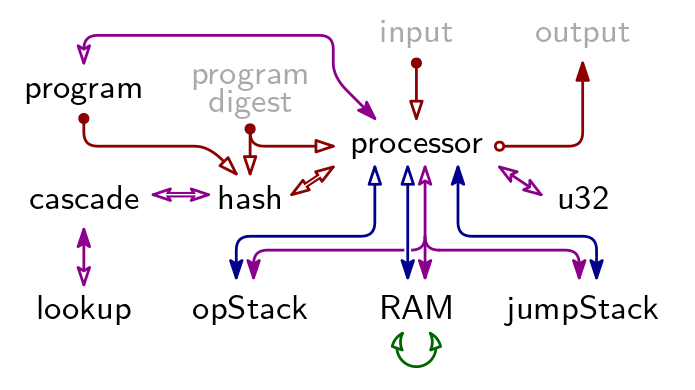
Base Tables

The values of all registers, and consequently the elements on the stack, in memory, and so on, are elements of the B-field, i.e., ${\mathbb{F}}_p$ where $p$ is the Oxfoi prime, $2^{64}-2^{32}+1$. All values of columns corresponding to one such register are elements of the B-Field as well. Together, these columns are referred to as table's base columns, and make up the base table.

Extension Tables

The entries of a table's columns corresponding to Permutation, Evaluation, and Lookup Arguments are elements from the X-field ${\mathbb{F}}_{p^3}$. These columns are referred to as a table's extension columns, both because the entries are elements of the X-field and because the entries can only be computed using the base tables, through an extension process. Together, these columns are referred to as a table's extension columns, and make up the extension table.

Padding

For reasons of computational efficiency, it is beneficial that an Algebraic Execution Table's height equals a power of 2. To this end, tables are padded. The height $h$ of the longest AET determines the padded height for all tables, which is $2^{\lceil {\log }_{2}h\rceil }$.

Arithmetic Intermediate Representation

For each table, up to four lists containing constraints of different type are given:

1. Initial Constraints, defining values in a table's first row,
2. Consistency Constraints, establishing consistency within any given row,
3. Transition Constraints, establishing the consistency of two consecutive rows in relation to each other, and
4. Terminal Constraints, defining values in a table's last row.

Together, all these constraints constitute the AIR constraints.

Arguments Using Public Information

Triton VM uses a number of public arguments. That is, one side of the link can be computed by the verifier using publicly available information; the other side of the link is verified through one or more AIR constraints.

The two most prominent instances of this are public input and output: both are given to the verifier explicitly. The verifier can compute the terminal of an Evaluation Argument using public input (respectively, output). In the Processor Table, AIR constraints guarantee that the used input (respectively, output) symbols are accumulated similarly. Comparing the two terminal values establishes that use of public input (respectively, production of public output) was integral.

The third public argument establishes correctness of the Lookup Table, and is explained there. The fourth public argument relates to program attestation, and is also explained on its corresponding page.

Program Table

The Program Table contains the entire program as a read-only list of instruction opcodes and their arguments. The processor looks up instructions and arguments using its instruction pointer ip.

For program attestation, the program is padded and sent to the Hash Table in chunks of size 10, which is the $\text{rate}$ of the Tip5 hash function. Program padding is one 1 followed by the minimal number of 0’s necessary to make the padded input length a multiple of the $\text{rate}$¹.

Base Columns

The Program Table consists of 7 base columns. Those columns marked with an asterisk (*) are only used for program attestation.

Extension Columns

A Lookup Argument with the Processor Table establishes that the processor has loaded the correct instruction (and its argument) from program memory. To establish the program memory's side of the Lookup Argument, the Program Table has extension column InstructionLookupServerLogDerivative.

For sending the padded program to the Hash Table, a combination of two Evaluation Arguments is used. The first, PrepareChunkRunningEvaluation, absorbs one chunk of $\text{rate}$ (i.e. 10) instructions at a time, after which it is reset and starts absorbing again. The second, SendChunkRunningEvaluation, absorbs one such prepared chunk every 10 instructions.

Padding

A padding row is a copy of the Program Table's last row with the following modifications:

1. column Address is increased by 1,
2. column Instruction is set to 0,
3. column LookupMultiplicity is set to 0,
4. column IndexInChunk is set to Address mod $\text{rate}$,
5. column MaxMinusIndexInChunkInv is set to the inverse-or-zero of $\text{rate}-1-\text{IndexInChunk}$,
6. column IsHashInputPadding is set to 1, and
7. column IsTablePadding is set to 1.

Above procedure is iterated until the necessary number of rows have been added.

A Note on the Instruction Lookup Argument

For almost all table-linking arguments, the initial row contains the argument's initial value after having applied the first update. For example, the initial row for a Lookup Argument usually contains $\frac{x}{\alpha -y}$ for some $x$ and $y$. As an exception, the Program Table's instruction Lookup Argument always records 0 in the initial row.

Recall that the Lookup Argument is not just about the instruction, but also about the instruction's argument if it has one, or the next instruction if it has none. In the Program Table, this argument (or the next instruction) is recorded in the next row from the instruction in question. Therefore, verifying correct application of the logarithmic derivative's update rule requires access to both the current and the next row.

Out of all constraint types, only Transition Constraints have access to more than one row at a time. This implies that the correct application of the first update of the instruction Lookup Argument cannot be verified by an initial constraint. Therefore, the recorded initial value must be independent of the second row.

Consequently, the final value for the Lookup Argument is recorded in the first row just after the program description ends. This row is guaranteed to exist because of the mechanics for program attestation: the program has to be padded with at least one 1 before it is hashed.

Arithmetic Intermediate Representation

Let all household items (🪥, 🛁, etc.) be challenges, concretely evaluation points, supplied by the verifier. Let all fruit & vegetables (🥝, 🥥, etc.) be challenges, concretely weights to compress rows, supplied by the verifier. Both types of challenges are X-field elements, i.e., elements of ${\mathbb{F}}_{p^3}$.

Initial Constraints

1. The Address is 0.
2. The IndexInChunk is 0.
3. The indicator IsHashInputPadding is 0.
4. The InstructionLookupServerLogDerivative is 0.
5. PrepareChunkRunningEvaluation has absorbed Instruction with respect to challenge 🪑.
6. SendChunkRunningEvaluation is 1.

Initial Constraints as Polynomials

1. Address
2. IndexInChunk
3. IsHashInputPadding
4. InstructionLookupServerLogDerivative
5. PrepareChunkRunningEvaluation - 🪑 - Instruction
6. SendChunkRunningEvaluation - 1

Consistency Constraints

1. The MaxMinusIndexInChunkInv is zero or the inverse of $\text{rate}-1-$ IndexInChunk.
2. The IndexInChunk is $\text{rate}-1$ or the MaxMinusIndexInChunkInv is the inverse of $\text{rate}-1-$ IndexInChunk.
3. Indicator IsHashInputPadding is either 0 or 1.
4. Indicator IsTablePadding is either 0 or 1.

Consistency Constraints as Polynomials

1. (1 - MaxMinusIndexInChunkInv · (rate - 1 - IndexInChunk)) · MaxMinusIndexInChunkInv
2. (1 - MaxMinusIndexInChunkInv · (rate - 1 - IndexInChunk)) · (rate - 1 - IndexInChunk)
3. IsHashInputPadding · (IsHashInputPadding - 1)
4. IsTablePadding · (IsTablePadding - 1)

Transition Constraints

1. The Address increases by 1.
2. If the IndexInChunk is not $\text{rate}-1$, it increases by 1. Else, the IndexInChunk in the next row is 0.
3. The indicator IsHashInputPadding is 0 or remains unchanged.
4. The padding indicator IsTablePadding is 0 or remains unchanged.
5. If IsHashInputPadding is 0 in the current row and 1 in the next row, then Instruction in the next row is 1.
6. If IsHashInputPadding is 1 in the current row then Instruction in the next row is 0.
7. If IsHashInputPadding is 1 in the current row and IndexInChunk is $\text{rate}-1$ in the current row then IsTablePadding is 1 in the next row.
8. If the current row is not a padding row, the logarithmic derivative accumulates the current row's address, the current row's instruction, and the next row's instruction with respect to challenges 🥝, 🥥, and 🫐 and indeterminate 🪥 respectively. Otherwise, it remains unchanged.
9. If the IndexInChunk in the current row is not $\text{rate}-1$, then PrepareChunkRunningEvaluation absorbs the Instruction in the next row with respect to challenge 🪑. Otherwise, PrepareChunkRunningEvaluation resets and absorbs the Instruction in the next row with respect to challenge 🪑.
10. If the next row is not a padding row and the IndexInChunk in the next row is $\text{rate}-1$, then SendChunkRunningEvaluation absorbs PrepareChunkRunningEvaluation in the next row with respect to variable 🪣. Otherwise, it remains unchanged.

Transition Constraints as Polynomials

1. Address' - Address - 1
2. MaxMinusIndexInChunkInv · (IndexInChunk' - IndexInChunk - 1)
+ (1 - MaxMinusIndexInChunkInv · (rate - 1 - IndexInChunk)) · IndexInChunk'
3. IsHashInputPadding · (IsHashInputPadding' - IsHashInputPadding)
4. IsTablePadding · (IsTablePadding' - IsTablePadding)
5. (IsHashInputPadding - 1) · IsHashInputPadding' · (Instruction' - 1)
6. IsHashInputPadding · Instruction'
7. IsHashInputPadding · (1 - MaxMinusIndexInChunkInv · (rate - 1 - IndexInChunk)) · IsTablePadding'
8. (1 - IsHashInputPadding) · ((InstructionLookupServerLogDerivative' - InstructionLookupServerLogDerivative) · (🪥 - 🥝·Address - 🥥·Instruction - 🫐·Instruction') - LookupMultiplicity)
+ IsHashInputPadding · (InstructionLookupServerLogDerivative' - InstructionLookupServerLogDerivative)
9. (rate - 1 - IndexInChunk) · (PrepareChunkRunningEvaluation' - 🪑·PrepareChunkRunningEvaluation - Instruction')
+ (1 - MaxMinusIndexInChunkInv · (rate - 1 - IndexInChunk)) · (PrepareChunkRunningEvaluation' - 🪑 - Instruction')
10. (IsTablePadding' - 1) · (1 - MaxMinusIndexInChunkInv' · (rate - 1 - IndexInChunk')) · (SendChunkRunningEvaluation' - 🪣·SendChunkRunningEvaluation - PrepareChunkRunningEvaluation')
+ (SendChunkRunningEvaluation' - SendChunkRunningEvaluation) · IsTablePadding'
+ (SendChunkRunningEvaluation' - SendChunkRunningEvaluation) · (rate - 1 - IndexInChunk')
    

Terminal Constraints

1. The indicator IsHashInputPadding is 1.
2. The IndexInChunk is $\text{rate}-1$ or the indicator IsTablePadding is 1.

Terminal Constraints as Polynomials

1. IsHashInputPadding - 1
2. (rate - 1 - IndexInChunk) · (IsTablePadding - 1)

Processor Table

The Processor Table records all of Triton VM states during execution of a particular program. The states are recorded in chronological order. The first row is the initial state, the last (non-padding) row is the terminal state, i.e., the state after having executed instruction halt. It is impossible to generate a valid proof if the instruction executed last is anything but halt.

It is worth highlighting the initialization of the operational stack. Stack elements st0 through st10 are initially 0. However, stack elements st11 through st15, i.e., the very bottom of the stack, are initialized with the hash digest of the program that is being executed. This is primarily useful for recursive verifiers: they can compare their own program digest to the program digest of the proof they are verifying. This way, a recursive verifier can easily determine if they are actually recursing, or whether the proof they are checking was generated using an entirely different program. A more detailed explanation of the mechanics can be found on the page about program attestation.

Base Columns

The processor consists of all registers defined in the Instruction Set Architecture. Each register is assigned a column in the processor table.

Extension Columns

The Processor Table has the following extension columns, corresponding to Evaluation Arguments, Permutation Arguments, and Lookup Arguments:

1. RunningEvaluationStandardInput for the Evaluation Argument with the input symbols.
2. RunningEvaluationStandardOutput for the Evaluation Argument with the output symbols.
3. InstructionLookupClientLogDerivative for the Lookup Argument with the Program Table
4. RunningProductOpStackTable for the Permutation Argument with the OpStack Table.
5. RunningProductRamTable for the Permutation Argument with the RAM Table.
6. RunningProductJumpStackTable for the Permutation Argument with the Jump Stack Table.
7. RunningEvaluationHashInput for the Evaluation Argument with the Hash Table for copying the input to the hash function from the processor to the hash coprocessor.
8. RunningEvaluationHashDigest for the Evaluation Argument with the Hash Table for copying the hash digest from the hash coprocessor to the processor.
9. RunningEvaluationSponge for the Evaluation Argument with the Hash Table for copying the 10 next to-be-absorbed elements from the processor to the hash coprocessor or the 10 next squeezed elements from the hash coprocessor to the processor, depending on the instruction.
10. U32LookupClientLogDerivative for the Lookup Argument with the U32 Table.
11. ClockJumpDifferenceLookupServerLogDerivative for the Lookup Argument of clock jump differences with the OpStack Table, the RAM Table, and the JumpStack Table.

Padding

A padding row is a copy of the Processor Table's last row with the following modifications:

1. column clk is increased by 1,
2. column IsPadding is set to 1,
3. column cjd_mul is set to 0,

A notable exception: if the row with clk equal to 1 is a padding row, then the value of cjd_mul is not constrained in that row. The reason for this exception is the lack of “awareness” of padding rows in the three memory-like tables. In fact, all memory-like tables keep looking up clock jump differences in their padding section. All these clock jumps are guaranteed to have magnitude 1 due to the Permutation Arguments with the respective memory-like tables.

Arithmetic Intermediate Representation

Let all household items (🪥, 🛁, etc.) be challenges, concretely evaluation points, supplied by the verifier. Let all fruit & vegetables (🥝, 🥥, etc.) be challenges, concretely weights to compress rows, supplied by the verifier. Both types of challenges are X-field elements, i.e., elements of ${\mathbb{F}}_{p^3}$.

Note, that the transition constraint's use of some_column vs some_column_next might be a little unintuitive. For example, take the following part of some execution trace.

In order to verify the correctness of RunningEvaluationHashInput, the corresponding transition constraint needs to conditionally “activate” on row-tuple ($i-1$, $i$), where it is conditional on ci_next (not ci), and verifies absorption of the next row, i.e., row $i$. However, in order to verify the correctness of RunningEvaluationHashDigest, the corresponding transition constraint needs to conditionally “activate” on row-tuple ($i$, $i+1$), where it is conditional on ci (not ci_next), and verifies absorption of the next row, i.e., row $i+1$.

Initial Constraints

1. The cycle counter clk is 0.
2. The previous instruction previous_instruction is 0.
3. The instruction pointer ip is 0.
4. The jump address stack pointer jsp is 0.
5. The jump address origin jso is 0.
6. The jump address destination jsd is 0.
7. The operational stack element st0 is 0.
8. The operational stack element st1 is 0.
9. The operational stack element st2 is 0.
10. The operational stack element st3 is 0.
11. The operational stack element st4 is 0.
12. The operational stack element st5 is 0.
13. The operational stack element st6 is 0.
14. The operational stack element st7 is 0.
15. The operational stack element st8 is 0.
16. The operational stack element st9 is 0.
17. The operational stack element st10 is 0.
18. The Evaluation Argument of operational stack elements st11 through st15 with respect to indeterminate 🥬 equals the public part of program digest challenge, 🫑. See program attestation for more details.
19. The operational stack pointer osp is 16.
20. The operational stack value osv is 0.
21. The RAM pointer ramp is 0.
22. RunningEvaluationStandardInput is 1.
23. RunningEvaluationStandardOutput is 1.
24. InstructionLookupClientLogDerivative has absorbed the first row with respect to challenges 🥝, 🥥, and 🫐 and indeterminate 🪥.
25. RunningProductOpStackTable has absorbed the first row with respect to challenges 🍋, 🍊, 🍉, and 🫒 and indeterminate 🪤.
26. RunningProductRamTable has absorbed the first row with respect to challenges 🍍, 🍈, 🍎, and 🌽 and indeterminate 🛋.
27. RunningProductJumpStackTable has absorbed the first row with respect to challenges 🍇, 🍅, 🍌, 🍏, and 🍐 and indeterminate 🧴.
28. RunningEvaluationHashInput has absorbed the first row with respect to challenges 🧄₀ through 🧄₉ and indeterminate 🚪 if the current instruction is hash. Otherwise, it is 1.
29. RunningEvaluationHashDigest is 1.
30. RunningEvaluationSponge is 1.
31. U32LookupClientLogDerivative is 0.
32. ClockJumpDifferenceLookupServerLogDerivative is 0.

Initial Constraints as Polynomials

1. clk
2. previous_instruction
3. ip
4. jsp
5. jso
6. jsd
7. st0
8. st1
9. st2
10. st3
11. st4
12. st5
13. st6
14. st7
15. st8
16. st9
17. st10
18. 🥬^5 + st11·🥬^4 + st12·🥬^3 + st13·🥬^2 + st14·🥬 + st15 - 🫑
19. osp
20. osv
21. ramp
22. RunningEvaluationStandardInput - 1
23. RunningEvaluationStandardOutput - 1
24. InstructionLookupClientLogDerivative · (🪥 - 🥝·ip - 🥥·ci - 🫐·nia) - 1
25. RunningProductOpStackTable - (🪤 - 🍋·clk - 🍊·ib1 - 🍉·osp - 🫒·osv)
26. RunningProductRamTable - (🛋 - 🍍·clk - 🍈·ramp - 🍎·ramv - 🌽·previous_instruction)
27. RunningProductJumpStackTable - (🧴 - 🍇·clk - 🍅·ci - 🍌·jsp - 🍏·jso - 🍐·jsd)
28. (ci - opcode(hash))·(RunningEvaluationHashInput - 1)
+ hash_deselector·(RunningEvaluationHashInput - 🚪 - 🧄₀·st0 - 🧄₁·st1 - 🧄₂·st2 - 🧄₃·st3 - 🧄₄·st4 - 🧄₅·st5 - 🧄₆·st6 - 🧄₇·st7 - 🧄₈·st8 - 🧄₉·st9)
29. RunningEvaluationHashDigest - 1
30. RunningEvaluationSponge - 1
31. U32LookupClientLogDerivative
32. ClockJumpDifferenceLookupServerLogDerivative

Consistency Constraints

1. The composition of instruction bits ib0 through ib7 corresponds to the current instruction ci.
2. The instruction bit ib0 is a bit.
3. The instruction bit ib1 is a bit.
4. The instruction bit ib2 is a bit.
5. The instruction bit ib3 is a bit.
6. The instruction bit ib4 is a bit.
7. The instruction bit ib5 is a bit.
8. The instruction bit ib6 is a bit.
9. The instruction bit ib7 is a bit.
10. The padding indicator IsPadding is either 0 or 1.
11. If the current padding row is a padding row and clk is not 1, then the clock jump difference lookup multiplicity is 0.

Consistency Constraints as Polynomials

1. ci - (2^7·ib7 + 2^6·ib6 + 2^5·ib5 + 2^4·ib4 + 2^3·ib3 + 2^2·ib2 + 2^1·ib1 + 2^0·ib0)
2. ib0·(ib0 - 1)
3. ib1·(ib1 - 1)
4. ib2·(ib2 - 1)
5. ib3·(ib3 - 1)
6. ib4·(ib4 - 1)
7. ib5·(ib5 - 1)
8. ib6·(ib6 - 1)
9. ib7·(ib7 - 1)
10. IsPadding·(IsPadding - 1)
11. IsPadding·(clk - 1)·ClockJumpDifferenceLookupServerLogDerivative

Transition Constraints

Due to their complexity, instruction-specific constraints are defined in their own section. The following additional constraints also apply to every pair of rows.

1. The cycle counter clk increases by 1.
2. The padding indicator IsPadding is 0 or remains unchanged.
3. The current instruction ci in the current row is copied into previous_instruction in the next row or the next row is a padding row.
4. The running evaluation for standard input absorbs st0 of the next row with respect to 🛏 if the current instruction is read_io, and remains unchanged otherwise.
5. The running evaluation for standard output absorbs st0 of the next row with respect to 🧯 if the current instruction in the next row is write_io, and remains unchanged otherwise.
6. If the next row is not a padding row, the logarithmic derivative for the Program Table absorbs the next row with respect to challenges 🥝, 🥥, and 🫐 and indeterminate 🪥. Otherwise, it remains unchanged.
7. The running product for the OpStack Table absorbs the next row with respect to challenges 🍋, 🍊, 🍉, and 🫒 and indeterminate 🪤.
8. The running product for the RAM Table absorbs the next row with respect to challenges 🍍, 🍈, 🍎, and 🌽 and indeterminate 🛋.
9. The running product for the JumpStack Table absorbs the next row with respect to challenges 🍇, 🍅, 🍌, 🍏, and 🍐 and indeterminate 🧴.
10. If the current instruction in the next row is hash, the running evaluation “Hash Input” absorbs the next row with respect to challenges 🧄₀ through 🧄₉ and indeterminate 🚪. Otherwise, it remains unchanged.
11. If the current instruction is hash, the running evaluation “Hash Digest” absorbs the next row with respect to challenges 🧄₀ through 🧄₄ and indeterminate 🪟. Otherwise, it remains unchanged.
12. If the current instruction is absorb_init, absorb, or squeeze, then the running evaluation “Sponge” absorbs the current instruction and the next row with respect to challenges 🧅 and 🧄₀ through 🧄₉ and indeterminate 🧽. Otherwise, it remains unchanged.
13. 1. If the current instruction is split, then the logarithmic derivative for the Lookup Argument with the U32 Table accumulates st0 and st1 in the next row and ci in the current row with respect to challenges 🥜, 🌰, and 🥑, and indeterminate 🧷.
    2. If the current instruction is lt, and, xor, or pow, then the logarithmic derivative for the Lookup Argument with the U32 Table accumulates st0, st1, and ci in the current row and st0 in the next row with respect to challenges 🥜, 🌰, 🥑, and 🥕, and indeterminate 🧷.
    3. If the current instruction is log_2_floor, then the logarithmic derivative for the Lookup Argument with the U32 Table accumulates st0 and ci in the current row and st0 in the next row with respect to challenges 🥜, 🥑, and 🥕, and indeterminate 🧷.
    4. If the current instruction is div, then the logarithmic derivative for the Lookup Argument with the U32 Table accumulates both
       1. st0 in the next row and st1 in the current row as well as the constants opcode(lt) and 1 with respect to challenges 🥜, 🌰, 🥑, and 🥕, and indeterminate 🧷.
       2. st0 in the current row and st1 in the next row as well as opcode(split) with respect to challenges 🥜, 🌰, and 🥑, and indeterminate 🧷.
    5. If the current instruction is pop_count, then the logarithmic derivative for the Lookup Argument with the U32 Table accumulates st0 and ci in the current row and st0 in the next row with respect to challenges 🥜, 🥑, and 🥕, and indeterminate 🧷.
    6. Else, i.e., if the current instruction is not a u32 instruction, the logarithmic derivative for the Lookup Argument with the U32 Table remains unchanged.
14. The running sum for the logarithmic derivative of the clock jump difference lookup argument accumulates the next row's clk with the appropriate multiplicity cjd_mul with respect to indeterminate 🪞.

Transition Constraints as Polynomials

1. clk' - (clk + 1)
2. IsPadding·(IsPadding' - IsPadding)
3. (1 - IsPadding')·(previous_instruction' - ci)
4. (ci - opcode(read_io))·(RunningEvaluationStandardInput' - RunningEvaluationStandardInput)
+ read_io_deselector·(RunningEvaluationStandardInput' - 🛏·RunningEvaluationStandardInput - st0')
5. (ci' - opcode(write_io))·(RunningEvaluationStandardOutput' - RunningEvaluationStandardOutput)
+ write_io_deselector'·(RunningEvaluationStandardOutput' - 🧯·RunningEvaluationStandardOutput - st0')
6. (1 - IsPadding') · ((InstructionLookupClientLogDerivative' - InstructionLookupClientLogDerivative) · (🛁 - 🥝·ip' - 🥥·ci' - 🫐·nia') - 1)
+ IsPadding'·(RunningProductInstructionTable' - RunningProductInstructionTable)
7. RunningProductOpStackTable' - RunningProductOpStackTable·(🪤 - 🍋·clk' - 🍊·ib1' - 🍉·osp' - 🫒·osv')
8. RunningProductRamTable' - RunningProductRamTable·(🛋 - 🍍·clk' - 🍈·ramp' - 🍎·ramv' - 🌽·previous_instruction')
9. RunningProductJumpStackTable' - RunningProductJumpStackTable·(🧴 - 🍇·clk' - 🍅·ci' - 🍌·jsp' - 🍏·jso' - 🍐·jsd')
10. (ci' - opcode(hash))·(RunningEvaluationHashInput' - RunningEvaluationHashInput)
+ hash_deselector'·(RunningEvaluationHashInput' - 🚪·RunningEvaluationHashInput - 🧄₀·st0' - 🧄₁·st1' - 🧄₂·st2' - 🧄₃·st3' - 🧄₄·st4' - 🧄₅·st5' - 🧄₆·st6' - 🧄₇·st7' - 🧄₈·st8' - 🧄₉·st9')
11. (ci - opcode(hash))·(RunningEvaluationHashDigest' - RunningEvaluationHashDigest)
+ hash_deselector·(RunningEvaluationHashDigest' - 🪟·RunningEvaluationHashDigest - 🧄₀·st5' - 🧄₁·st6' - 🧄₂·st7' - 🧄₃·st8' - 🧄₄·st9')
12. (ci - opcode(absorb_init))·(ci - opcode(absorb)·(ci - opcode(squeeze))·(RunningEvaluationHashDigest' - RunningEvaluationHashDigest)
+ (absorb_init_deselector + absorb_deselector + squeeze_deselector)
·(RunningEvaluationSponge' - 🧽·RunningEvaluationSponge - 🧅·ci - 🧄₀·st0' - 🧄₁·st1' - 🧄₂·st2' - 🧄₃·st3' - 🧄₄·st4' - 🧄₅·st5' - 🧄₆·st6' - 🧄₇·st7' - 🧄₈·st8' - 🧄₉·st9')
13. 1. split_deselector·((U32LookupClientLogDerivative' - U32LookupClientLogDerivative)·(🧷 - 🥜·st0' - 🌰·st1' - 🥑·ci) - 1)
    2. + lt_deselector·((U32LookupClientLogDerivative' - U32LookupClientLogDerivative)·(🧷 - 🥜·st0 - 🌰·st1 - 🥑·ci - 🥕·st0') - 1)
    3. + and_deselector·((U32LookupClientLogDerivative' - U32LookupClientLogDerivative)·(🧷 - 🥜·st0 - 🌰·st1 - 🥑·ci - 🥕·st0') - 1)
    4. + xor_deselector·((U32LookupClientLogDerivative' - U32LookupClientLogDerivative)·(🧷 - 🥜·st0 - 🌰·st1 - 🥑·ci - 🥕·st0') - 1)
    5. + pow_deselector·((U32LookupClientLogDerivative' - U32LookupClientLogDerivative)·(🧷 - 🥜·st0 - 🌰·st1 - 🥑·ci - 🥕·st0') - 1)
    6. + log_2_floor_deselector·((U32LookupClientLogDerivative' - U32LookupClientLogDerivative)·(🧷 - 🥜·st0 - 🥑·ci - 🥕·st0') - 1)
    7. + div_deselector·(
  (U32LookupClientLogDerivative' - U32LookupClientLogDerivative)·(🧷 - 🥜·st0' - 🌰·st1 - 🥑·opcode(lt) - 🥕·1)·(🧷 - 🥜·st0 - 🌰·st1' - 🥑·opcode(split))
  - (🧷 - 🥜·st0' - 🌰·st1 - 🥑·opcode(lt) - 🥕·1)
  - (🧷 - 🥜·st0 - 🌰·st1' - 🥑·opcode(split))
 )
    8. + pop_count_deselector·((U32LookupClientLogDerivative' - U32LookupClientLogDerivative)·(🧷 - 🥜·st0 - 🥑·ci - 🥕·st0') - 1)
    9. + (1 - ib2)·(U32LookupClientLogDerivative' - U32LookupClientLogDerivative)
14. (ClockJumpDifferenceLookupServerLogDerivative' - ClockJumpDifferenceLookupServerLogDerivative)
·(🪞 - clk') - cjd_mul'

Terminal Constraints

1. In the last row, register “current instruction” ci is 0, corresponding to instruction halt.

Terminal Constraints as Polynomials

1. ci

Instruction Groups

Some transition constraints are shared across some, or even many instructions. For example, most instructions must not change the jump stack. Likewise, most instructions must not change RAM. To simplify presentation of the instruction-specific transition constraints, these common constraints are grouped together and aliased. Continuing above example, instruction group keep_jump_stack contains all transition constraints to ensure that the jump stack remains unchanged.

The next section treats each instruction group in detail. The following table lists and briefly explains all instruction groups.

Below figure gives a comprehensive overview over the subset relation between all instruction groups.

A summary of all instructions and which groups they are part of is given in the following table.

Indicator Polynomials ind_i(hv3, hv2, hv1, hv0)

In this and the following sections, a register marked with a ' refers to the next state of that register. For example, st0' = st0 + 2 means that stack register st0 is incremented by 2. An alternative view for the same concept is that registers marked with ' are those of the next row in the table.

For instructions dup and swap, it is beneficial to have polynomials that evaluate to 1 if the instruction's argument i is a specific value, and to 0 otherwise. This allows indicating which registers are constraint, and in which way they are, depending on i. This is the purpose of the indicator polynomials ind_i. Evaluated on the binary decomposition of i, they show the behavior described above.

For example, take i = 13. The corresponding binary decomposition is (hv3, hv2, hv1, hv0) = (1, 1, 0, 1). Indicator polynomial ind_13(hv3, hv2, hv1, hv0) is hv3·hv2·(1 - hv1)·hv0. It evaluates to 1 on (1, 1, 0, 1), i.e., ind_13(1, 1, 0, 1) = 1. Any other indicator polynomial, like ind_7, evaluates to 0 on (1, 1, 0, 1). Likewise, the indicator polynomial for 13 evaluates to 0 for any other argument.

Below, you can find a list of all 16 indicator polynomials.

1. ind_0(hv3, hv2, hv1, hv0) = (1 - hv3)·(1 - hv2)·(1 - hv1)·(1 - hv0)
2. ind_1(hv3, hv2, hv1, hv0) = (1 - hv3)·(1 - hv2)·(1 - hv1)·hv0
3. ind_2(hv3, hv2, hv1, hv0) = (1 - hv3)·(1 - hv2)·hv1·(1 - hv0)
4. ind_3(hv3, hv2, hv1, hv0) = (1 - hv3)·(1 - hv2)·hv1·hv0
5. ind_4(hv3, hv2, hv1, hv0) = (1 - hv3)·hv2·(1 - hv1)·(1 - hv0)
6. ind_5(hv3, hv2, hv1, hv0) = (1 - hv3)·hv2·(1 - hv1)·hv0
7. ind_6(hv3, hv2, hv1, hv0) = (1 - hv3)·hv2·hv1·(1 - hv0)
8. ind_7(hv3, hv2, hv1, hv0) = (1 - hv3)·hv2·hv1·hv0
9. ind_8(hv3, hv2, hv1, hv0) = hv3·(1 - hv2)·(1 - hv1)·(1 - hv0)
10. ind_9(hv3, hv2, hv1, hv0) = hv3·(1 - hv2)·(1 - hv1)·hv0
11. ind_10(hv3, hv2, hv1, hv0) = hv3·(1 - hv2)·hv1·(1 - hv0)
12. ind_11(hv3, hv2, hv1, hv0) = hv3·(1 - hv2)·hv1·hv0
13. ind_12(hv3, hv2, hv1, hv0) = hv3·hv2·(1 - hv1)·(1 - hv0)
14. ind_13(hv3, hv2, hv1, hv0) = hv3·hv2·(1 - hv1)·hv0
15. ind_14(hv3, hv2, hv1, hv0) = hv3·hv2·hv1·(1 - hv0)
16. ind_15(hv3, hv2, hv1, hv0) = hv3·hv2·hv1·hv0

Group decompose_arg

Description

1. The helper variables are the decomposition of the instruction's argument, which is held in register nia.
2. The helper variable hv0 is either 0 or 1.
3. The helper variable hv1 is either 0 or 1.
4. The helper variable hv2 is either 0 or 1.
5. The helper variable hv3 is either 0 or 1.

Polynomials

1. nia - (8·hv3 + 4·hv2 + 2·hv1 + hv0)
2. hv0·(hv0 - 1)
3. hv1·(hv1 - 1)
4. hv2·(hv2 - 1)
5. hv3·(hv3 - 1)

Group keep_ram

Description

1. The RAM pointer ramp does not change.
2. The RAM value ramv does not change.

Polynomials

1. ramp' - ramp
2. ramv' - ramv

Group keep_jump_stack

Description

1. The jump stack pointer jsp does not change.
2. The jump stack origin jso does not change.
3. The jump stack destination jsd does not change.

Polynomials

1. jsp' - jsp
2. jso' - jso
3. jsd' - jsd

Group step_1

Contains all constraints from instruction group keep_jump_stack, and additionally:

Description

1. The instruction pointer increments by 1.

Polynomials

1. ip' - (ip + 1)

Group step_2

Contains all constraints from instruction group keep_jump_stack, and additionally:

Description

1. The instruction pointer increments by 2.

Polynomials

1. ip' - (ip + 2)

Group stack_grows_and_top_2_unconstrained

Description

1. The stack element in st1 is moved into st2.
2. The stack element in st2 is moved into st3.
3. The stack element in st3 is moved into st4.
4. The stack element in st4 is moved into st5.
5. The stack element in st5 is moved into st6.
6. The stack element in st6 is moved into st7.
7. The stack element in st7 is moved into st8.
8. The stack element in st8 is moved into st9.
9. The stack element in st9 is moved into st10.
10. The stack element in st10 is moved into st11.
11. The stack element in st11 is moved into st12.
12. The stack element in st12 is moved into st13.
13. The stack element in st13 is moved into st14.
14. The stack element in st14 is moved into st15.
15. The stack element in st15 is moved to the top of OpStack underflow, i.e., osv.
16. The OpStack pointer is incremented by 1.

Polynomials

1. st2' - st1
2. st3' - st2
3. st4' - st3
4. st5' - st4
5. st6' - st5
6. st7' - st6
7. st8' - st7
8. st9' - st8
9. st10' - st9
10. st11' - st10
11. st12' - st11
12. st13' - st12
13. st14' - st13
14. st15' - st14
15. osv' - st15
16. osp' - (osp + 1)

Group grow_stack

Contains all constraints from instruction group stack_grows_and_top_2_unconstrained, and additionally:

Description

1. The stack element in st0 is moved into st1.

Polynomials

1. st1' - st0

Group stack_remains_and_top_11_unconstrained

Description

1. The stack element in st11 does not change.
2. The stack element in st12 does not change.
3. The stack element in st13 does not change.
4. The stack element in st14 does not change.
5. The stack element in st15 does not change.
6. The top of the OpStack underflow, i.e., osv, does not change.
7. The OpStack pointer does not change.

Polynomials

1. st11' - st11
2. st12' - st12
3. st13' - st13
4. st14' - st14
5. st15' - st15
6. osv' - osv
7. osp' - osp

Group stack_remains_and_top_10_unconstrained

Contains all constraints from instruction group stack_remains_and_top_11_unconstrained, and additionally:

Description

1. The stack element in st10 does not change.

Polynomials

1. st10' - st10

Group stack_remains_and_top_3_unconstrained

Contains all constraints from instruction group stack_remains_and_top_10_unconstrained, and additionally:

Description

1. The stack element in st3 does not change.
2. The stack element in st4 does not change.
3. The stack element in st5 does not change.
4. The stack element in st6 does not change.
5. The stack element in st7 does not change.
6. The stack element in st8 does not change.
7. The stack element in st9 does not change.

Polynomials

1. st3' - st3
2. st4' - st4
3. st5' - st5
4. st6' - st6
5. st7' - st7
6. st8' - st8
7. st9' - st9

Group unary_operation

Contains all constraints from instruction group stack_remains_and_top_3_unconstrained, and additionally:

Description

1. The stack element in st1 does not change.
2. The stack element in st2 does not change.

Polynomials

1. st1' - st1
2. st2' - st2

Group keep_stack

Contains all constraints from instruction group unary_operation, and additionally:

Description

1. The stack element in st0 does not change.

Polynomials

1. st0' - st0

Group stack_shrinks_and_top_3_unconstrained

This instruction group requires helper variable hv0 to hold the multiplicative inverse of (osp - 16). In effect, this means that the OpStack pointer can only be decremented if it is not 16, i.e., if OpStack Underflow Memory is not empty. Since the stack can only change by one element at a time, this prevents stack underflow.

Description

1. The stack element in st4 is moved into st3.
2. The stack element in st5 is moved into st4.
3. The stack element in st6 is moved into st5.
4. The stack element in st7 is moved into st6.
5. The stack element in st8 is moved into st7.
6. The stack element in st9 is moved into st8.
7. The stack element in st10 is moved into st9.
8. The stack element in st11 is moved into st10.
9. The stack element in st12 is moved into st11.
10. The stack element in st13 is moved into st12.
11. The stack element in st14 is moved into st13.
12. The stack element in st15 is moved into st14.
13. The stack element at the top of OpStack underflow, i.e., osv, is moved into st15.
14. The OpStack pointer is decremented by 1.
15. The helper variable register hv0 holds the inverse of (osp - 16).

Polynomials

1. st3' - st4
2. st4' - st5
3. st5' - st6
4. st6' - st7
5. st7' - st8
6. st8' - st9
7. st9' - st10
8. st10' - st11
9. st11' - st12
10. st12' - st13
11. st13' - st14
12. st14' - st15
13. st15' - osv
14. osp' - (osp - 1)
15. (osp - 16)·hv0 - 1

Group binary_operation

Contains all constraints from instruction group stack_shrinks_and_top_3_unconstrained, and additionally:

Description

1. The stack element in st2 is moved into st1.
2. The stack element in st3 is moved into st2.

Polynomials

1. st1' - st2
2. st2' - st3

Group shrink_stack

Contains all constraints from instruction group binary_operation, and additionally:

Description

1. The stack element in st1 is moved into st0.

Polynomials

1. st0' - st1

Instruction-Specific Transition Constraints

Instruction pop

This instruction uses all constraints defined by instruction groups step_1, shrink_stack, and keep_ram. It has no additional transition constraints.

Instruction push + a

This instruction uses all constraints defined by instruction groups step_2, grow_stack, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. The instruction's argument a is moved onto the stack.

Polynomials

1. st0' - nia

Instruction divine

This instruction uses all constraints defined by instruction groups step_2, grow_stack, and keep_ram. It has no additional transition constraints.

Instruction dup + i

This instruction makes use of indicator polynomials. For their definition, please refer to the corresponding section.

This instruction uses all constraints defined by instruction groups decompose_arg, step_2, grow_stack, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. If i is 0, then st0 is put on top of the stack.
2. If i is 1, then st1 is put on top of the stack.
3. If i is 2, then st2 is put on top of the stack.
4. If i is 3, then st3 is put on top of the stack.
5. If i is 4, then st4 is put on top of the stack.
6. If i is 5, then st5 is put on top of the stack.
7. If i is 6, then st6 is put on top of the stack.
8. If i is 7, then st7 is put on top of the stack.
9. If i is 8, then st8 is put on top of the stack.
10. If i is 9, then st9 is put on top of the stack.
11. If i is 10, then st10 is put on top of the stack.
12. If i is 11, then st11 is put on top of the stack.
13. If i is 12, then st12 is put on top of the stack.
14. If i is 13, then st13 is put on top of the stack.
15. If i is 14, then st14 is put on top of the stack.
16. If i is 15, then st15 is put on top of the stack.

Polynomials

1. ind_0(hv3, hv2, hv1, hv0)·(st0' - st0)
2. ind_1(hv3, hv2, hv1, hv0)·(st0' - st1)
3. ind_2(hv3, hv2, hv1, hv0)·(st0' - st2)
4. ind_3(hv3, hv2, hv1, hv0)·(st0' - st3)
5. ind_4(hv3, hv2, hv1, hv0)·(st0' - st4)
6. ind_5(hv3, hv2, hv1, hv0)·(st0' - st5)
7. ind_6(hv3, hv2, hv1, hv0)·(st0' - st6)
8. ind_7(hv3, hv2, hv1, hv0)·(st0' - st7)
9. ind_8(hv3, hv2, hv1, hv0)·(st0' - st8)
10. ind_9(hv3, hv2, hv1, hv0)·(st0' - st9)
11. ind_10(hv3, hv2, hv1, hv0)·(st0' - st10)
12. ind_11(hv3, hv2, hv1, hv0)·(st0' - st11)
13. ind_12(hv3, hv2, hv1, hv0)·(st0' - st12)
14. ind_13(hv3, hv2, hv1, hv0)·(st0' - st13)
15. ind_14(hv3, hv2, hv1, hv0)·(st0' - st14)
16. ind_15(hv3, hv2, hv1, hv0)·(st0' - st15)

Helper variable definitions for dup + i

For dup + i, helper variables contain the binary decomposition of i:

1. hv0 = i % 2
2. hv1 = (i >> 1) % 2
3. hv2 = (i >> 2) % 2
4. hv3 = (i >> 3) % 2

Instruction swap + i

This instruction makes use of indicator polynomials. For their definition, please refer to the corresponding section.

This instruction uses all constraints defined by instruction groups decompose_arg, step_2, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. Argument i is not 0.
2. If i is 1, then st0 is moved into st1.
3. If i is 2, then st0 is moved into st2.
4. If i is 3, then st0 is moved into st3.
5. If i is 4, then st0 is moved into st4.
6. If i is 5, then st0 is moved into st5.
7. If i is 6, then st0 is moved into st6.
8. If i is 7, then st0 is moved into st7.
9. If i is 8, then st0 is moved into st8.
10. If i is 9, then st0 is moved into st9.
11. If i is 10, then st0 is moved into st10.
12. If i is 11, then st0 is moved into st11.
13. If i is 12, then st0 is moved into st12.
14. If i is 13, then st0 is moved into st13.
15. If i is 14, then st0 is moved into st14.
16. If i is 15, then st0 is moved into st15.
17. If i is 1, then st1 is moved into st0.
18. If i is 2, then st2 is moved into st0.
19. If i is 3, then st3 is moved into st0.
20. If i is 4, then st4 is moved into st0.
21. If i is 5, then st5 is moved into st0.
22. If i is 6, then st6 is moved into st0.
23. If i is 7, then st7 is moved into st0.
24. If i is 8, then st8 is moved into st0.
25. If i is 9, then st9 is moved into st0.
26. If i is 10, then st10 is moved into st0.
27. If i is 11, then st11 is moved into st0.
28. If i is 12, then st12 is moved into st0.
29. If i is 13, then st13 is moved into st0.
30. If i is 14, then st14 is moved into st0.
31. If i is 15, then st15 is moved into st0.
32. If i is not 1, then st1 does not change.
33. If i is not 2, then st2 does not change.
34. If i is not 3, then st3 does not change.
35. If i is not 4, then st4 does not change.
36. If i is not 5, then st5 does not change.
37. If i is not 6, then st6 does not change.
38. If i is not 7, then st7 does not change.
39. If i is not 8, then st8 does not change.
40. If i is not 9, then st9 does not change.
41. If i is not 10, then st10 does not change.
42. If i is not 11, then st11 does not change.
43. If i is not 12, then st12 does not change.
44. If i is not 13, then st13 does not change.
45. If i is not 14, then st14 does not change.
46. If i is not 15, then st15 does not change.
47. The top of the OpStack underflow, i.e., osv, does not change.
48. The OpStack pointer does not change.

Polynomials

1. ind_0(hv3, hv2, hv1, hv0)
2. ind_1(hv3, hv2, hv1, hv0)·(st1' - st0)
3. ind_2(hv3, hv2, hv1, hv0)·(st2' - st0)
4. ind_3(hv3, hv2, hv1, hv0)·(st3' - st0)
5. ind_4(hv3, hv2, hv1, hv0)·(st4' - st0)
6. ind_5(hv3, hv2, hv1, hv0)·(st5' - st0)
7. ind_6(hv3, hv2, hv1, hv0)·(st6' - st0)
8. ind_7(hv3, hv2, hv1, hv0)·(st7' - st0)
9. ind_8(hv3, hv2, hv1, hv0)·(st8' - st0)
10. ind_9(hv3, hv2, hv1, hv0)·(st9' - st0)
11. ind_10(hv3, hv2, hv1, hv0)·(st10' - st0)
12. ind_11(hv3, hv2, hv1, hv0)·(st11' - st0)
13. ind_12(hv3, hv2, hv1, hv0)·(st12' - st0)
14. ind_13(hv3, hv2, hv1, hv0)·(st13' - st0)
15. ind_14(hv3, hv2, hv1, hv0)·(st14' - st0)
16. ind_15(hv3, hv2, hv1, hv0)·(st15' - st0)
17. ind_1(hv3, hv2, hv1, hv0)·(st0' - st1)
18. ind_2(hv3, hv2, hv1, hv0)·(st0' - st2)
19. ind_3(hv3, hv2, hv1, hv0)·(st0' - st3)
20. ind_4(hv3, hv2, hv1, hv0)·(st0' - st4)
21. ind_5(hv3, hv2, hv1, hv0)·(st0' - st5)
22. ind_6(hv3, hv2, hv1, hv0)·(st0' - st6)
23. ind_7(hv3, hv2, hv1, hv0)·(st0' - st7)
24. ind_8(hv3, hv2, hv1, hv0)·(st0' - st8)
25. ind_9(hv3, hv2, hv1, hv0)·(st0' - st9)
26. ind_10(hv3, hv2, hv1, hv0)·(st0' - st10)
27. ind_11(hv3, hv2, hv1, hv0)·(st0' - st11)
28. ind_12(hv3, hv2, hv1, hv0)·(st0' - st12)
29. ind_13(hv3, hv2, hv1, hv0)·(st0' - st13)
30. ind_14(hv3, hv2, hv1, hv0)·(st0' - st14)
31. ind_15(hv3, hv2, hv1, hv0)·(st0' - st15)
32. (1 - ind_1(hv3, hv2, hv1, hv0))·(st1' - st1)
33. (1 - ind_2(hv3, hv2, hv1, hv0))·(st2' - st2)
34. (1 - ind_3(hv3, hv2, hv1, hv0))·(st3' - st3)
35. (1 - ind_4(hv3, hv2, hv1, hv0))·(st4' - st4)
36. (1 - ind_5(hv3, hv2, hv1, hv0))·(st5' - st5)
37. (1 - ind_6(hv3, hv2, hv1, hv0))·(st6' - st6)
38. (1 - ind_7(hv3, hv2, hv1, hv0))·(st7' - st7)
39. (1 - ind_8(hv3, hv2, hv1, hv0))·(st8' - st8)
40. (1 - ind_9(hv3, hv2, hv1, hv0))·(st9' - st9)
41. (1 - ind_10(hv3, hv2, hv1, hv0))·(st10' - st10)
42. (1 - ind_11(hv3, hv2, hv1, hv0))·(st11' - st11)
43. (1 - ind_12(hv3, hv2, hv1, hv0))·(st12' - st12)
44. (1 - ind_13(hv3, hv2, hv1, hv0))·(st13' - st13)
45. (1 - ind_14(hv3, hv2, hv1, hv0))·(st14' - st14)
46. (1 - ind_15(hv3, hv2, hv1, hv0))·(st15' - st15)
47. osv' - osv
48. osp' - osp

Helper variable definitions for swap + i

For swap + i, helper variables contain the binary decomposition of i:

1. hv0 = i % 2
2. hv1 = (i >> 1) % 2
3. hv2 = (i >> 2) % 2
4. hv3 = (i >> 3) % 2

Instruction nop

This instruction uses all constraints defined by instruction groups step_1, keep_stack, and keep_ram. It has no additional transition constraints.

Instruction skiz

For the correct behavior of instruction skiz, the instruction pointer ip needs to increment by either 1, or 2, or 3. The concrete value depends on the top of the stack st0 and the next instruction, held in nia.

Helper variable hv1 helps with identifying whether st0 is 0. To this end, it holds the inverse-or-zero of st0, i.e., is 0 if and only if st0 is 0, and is the inverse of st0 otherwise.

Efficient arithmetization of instruction skiz makes use of one of the properties of opcodes. Concretely, the least significant bit of an opcode is 1 if and only if the instruction takes an argument. The arithmetization of skiz can incorporate this simple flag by decomposing nia into helper variable registers hv, similarly to how ci is (always) deconstructed into instruction bit registers ib. Correct decomposition is guaranteed by employing a range check.

This instruction uses all constraints defined by instruction groups keep_jump_stack, shrink_stack, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. Helper variable hv1 is the inverse of st0 or 0.
2. Helper variable hv1 is the inverse of st0 or st0 is 0.
3. The next instruction nia is decomposed into helper variables hv2 through hv6.
4. The indicator helper variable hv2 is either 0 or 1. Here, hv2 == 1 means that nia takes an argument.
5. The helper variable hv3 is either 0 or 1 or 2 or 3.
6. The helper variable hv4 is either 0 or 1 or 2 or 3.
7. The helper variable hv5 is either 0 or 1 or 2 or 3.
8. The helper variable hv6 is either 0 or 1 or 2 or 3.
9. If st0 is non-zero, register ip is incremented by 1. If st0 is 0 and nia takes no argument, register ip is incremented by 2. If st0 is 0 and nia takes an argument, register ip is incremented by 3.

Written as Disjunctive Normal Form, the last constraint can be expressed as:

10. (Register st0 is 0 or ip is incremented by 1), and (st0 has a multiplicative inverse or hv2 is 1 or ip is incremented by 2), and (st0 has a multiplicative inverse or hv2 is 0 or ip is incremented by 3).

Since the three cases are mutually exclusive, the three respective polynomials can be summed up into one.

Polynomials

1. (st0·hv1 - 1)·hv1
2. (st0·hv1 - 1)·st0
3. nia - hv2 - 2·hv3 - 8·hv4 - 32·hv5 - 128·hv6
4. hv2·(hv2 - 1)
5. hv3·(hv3 - 1)·(hv3 - 2)·(hv3 - 3)
6. hv4·(hv4 - 1)·(hv4 - 2)·(hv4 - 3)
7. hv5·(hv5 - 1)·(hv5 - 2)·(hv5 - 3)
8. hv6·(hv6 - 1)·(hv6 - 2)·(hv6 - 3)
9. (ip' - (ip + 1)·st0)
+ ((ip' - (ip + 2))·(st0·hv1 - 1)·(hv2 - 1))
+ ((ip' - (ip + 3))·(st0·hv1 - 1)·hv2)

Helper variable definitions for skiz

1. hv1 = inverse(st0) (if st0 ≠ 0)
2. hv2 = nia mod 2
3. hv3 = (nia >> 1) mod 4
4. hv4 = (nia >> 3) mod 4
5. hv5 = (nia >> 5) mod 4
6. hv6 = nia >> 7

Instruction call + d

This instruction uses all constraints defined by instruction groups keep_stack and keep_ram. Additionally, it defines the following transition constraints.

Description

1. The jump stack pointer jsp is incremented by 1.
2. The jump's origin jso is set to the current instruction pointer ip plus 2.
3. The jump's destination jsd is set to the instruction's argument d.
4. The instruction pointer ip is set to the instruction's argument d.

Polynomials

1. jsp' - (jsp + 1)
2. jso' - (ip + 2)
3. jsd' - nia
4. ip' - nia

Instruction return

This instruction uses all constraints defined by instruction groups keep_stack and keep_ram. Additionally, it defines the following transition constraints.

Description

1. The jump stack pointer jsp is decremented by 1.
2. The instruction pointer ip is set to the last call's origin jso.

Polynomials

1. jsp' - (jsp - 1)
2. ip' - jso

Instruction recurse

This instruction uses all constraints defined by instruction groups keep_jump_stack, keep_stack, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. The jump stack pointer jsp does not change.
2. The last jump's origin jso does not change.
3. The last jump's destination jsd does not change.
4. The instruction pointer ip is set to the last jump's destination jsd.

Polynomials

1. jsp' - jsp
2. jso' - jso
3. jsd' - jsd
4. ip' - jsd

Instruction assert

This instruction uses all constraints defined by instruction groups step_1, shrink_stack, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. The current top of the stack st0 is 1.

Polynomials

1. st0 - 1

Instruction halt

This instruction uses all constraints defined by instruction groups step_1, keep_stack, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. The instruction executed in the following step is instruction halt.

Polynomials

1. ci' - ci

Instruction read_mem

This instruction uses all constraints defined by instruction groups step_1 and grow_stack. Additionally, it defines the following transition constraints.

Description

1. The RAM pointer is overwritten with stack element st0.
2. The top of the stack is overwritten with the RAM value.

Polynomials

1. ramp' - st0
2. st0' - ramv

Instruction write_mem

This instruction uses all constraints defined by instruction groups step_1 and shrink_stack. Additionally, it defines the following transition constraints.

Description

1. The RAM pointer is overwritten with stack element st1.
2. The RAM value is overwritten with the top of the stack.

Polynomials

1. ramp' - st1
2. ramv' - st0

Instruction hash

This instruction uses all constraints defined by instruction groups step_1, stack_remains_and_top_10_unconstrained, and keep_ram. It has no additional transition constraints. Two Evaluation Arguments with the Hash Table guarantee correct transition.

Instruction divine_sibling

Recall that in a Merkle tree, the indices of left (respectively right) leafs have 0 (respectively 1) as their least significant bit. The first two polynomials achieve that helper variable hv0 holds the result of st10 mod 2. The third polynomial sets the new value of st10 to st10 div 2.

This instruction uses all constraints defined by instruction groups step_1, stack_remains_and_top_11_unconstrained, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. Helper variable hv0 is either 0 or 1.
2. The 11th stack register is shifted by 1 bit to the right.
3. If hv0 is 0, then st0 does not change.
4. If hv0 is 0, then st1 does not change.
5. If hv0 is 0, then st2 does not change.
6. If hv0 is 0, then st3 does not change.
7. If hv0 is 0, then st4 does not change.
8. If hv0 is 1, then st0 is copied to st5.
9. If hv0 is 1, then st1 is copied to st6.
10. If hv0 is 1, then st2 is copied to st7.
11. If hv0 is 1, then st3 is copied to st8.
12. If hv0 is 1, then st4 is copied to st9.

Polynomials

1. hv0·(hv0 - 1)
2. st10'·2 + hv0 - st10
3. (1 - hv0)·(st0' - st0) + hv0·(st5' - st0)
4. (1 - hv0)·(st1' - st1) + hv0·(st6' - st1)
5. (1 - hv0)·(st2' - st2) + hv0·(st7' - st2)
6. (1 - hv0)·(st3' - st3) + hv0·(st8' - st3)
7. (1 - hv0)·(st4' - st4) + hv0·(st9' - st4)

Helper variable definitions for divine_sibling

Since st10 contains the Merkle tree node index,

1. hv0 holds the result of st10 % 2 (the node index's least significant bit, indicating whether it is a left/right node).

Instruction assert_vector

This instruction uses all constraints defined by instruction groups step_1, keep_stack, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. Register st0 is equal to st5.
2. Register st1 is equal to st6.
3. Register st2 is equal to st7.
4. Register st3 is equal to st8.
5. Register st4 is equal to st9.

Polynomials

1. st5 - st0
2. st6 - st1
3. st7 - st2
4. st8 - st3
5. st9 - st4

Instruction absorb_init

This instruction uses all constraints defined by instruction groups step_1, keep_stack, and keep_ram. Beyond that, this instruction has no transition constraints. Instead, correct transition is guaranteed by the Hash Table.

Instruction absorb

This instruction uses all constraints defined by instruction groups step_1, keep_stack, and keep_ram. Beyond that, this instruction has no transition constraints. Instead, correct transition is guaranteed by the Hash Table.

Instruction squeeze

This instruction uses all constraints defined by instruction groups step_1, stack_remains_and_top_10_unconstrained, and keep_ram. Beyond that, this instruction has no transition constraints. Instead, correct transition is guaranteed by the Hash Table.

Instruction add

This instruction uses all constraints defined by instruction groups step_1, binary_operation, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. The sum of the top two stack elements is moved into the top of the stack.

Polynomials

1. st0' - (st0 + st1)

Instruction mul

This instruction uses all constraints defined by instruction groups step_1, binary_operation, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. The product of the top two stack elements is moved into the top of the stack.

Polynomials

1. st0' - st0·st1

Instruction invert

This instruction uses all constraints defined by instruction groups step_1, unary_operation, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. The top of the stack's inverse is moved into the top of the stack.

Polynomials

1. st0'·st0 - 1

Instruction eq

This instruction uses all constraints defined by instruction groups step_1, binary_operation, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. Helper variable hv1 is the inverse of the difference of the stack's two top-most elements or 0.
2. Helper variable hv1 is the inverse of the difference of the stack's two top-most elements or the difference is 0.
3. The new top of the stack is 1 if the difference between the stack's two top-most elements is not invertible, 0 otherwise.

Polynomials

1. hv1·(hv1·(st1 - st0) - 1)
2. (st1 - st0)·(hv1·(st1 - st0) - 1)
3. st0' - (1 - hv1·(st1 - st0))

Helper variable definitions for eq

1. hv1 = inverse(rhs - lhs) if rhs - lhs ≠ 0.
2. hv1 = 0 if rhs - lhs = 0.

Instruction split

This instruction uses all constraints defined by instruction groups step_1, stack_grows_and_top_2_unconstrained, and keep_ram. Additionally, it defines the following transition constraints. Part of the correct transition, namely the range check on the instruction's result, is guaranteed by the U32 Table.

Description

1. The top of the stack is decomposed as 32-bit chunks into the stack's top-most two elements.
2. Helper variable hv0 holds the inverse of $2^{32}-1$ subtracted from the high 32 bits or the low 32 bits are 0.

Polynomials

1. st0 - (2^32·st1' + st0')
2. st0'·(hv0·(st1' - (2^32 - 1)) - 1)

Helper variable definitions for split

Given the high 32 bits of st0 as hi = st0 >> 32 and the low 32 bits of st0 as lo = st0 & 0xffff_ffff,

1. hv0 = (hi - (2^32 - 1)) if lo ≠ 0.
2. hv0 = 0 if lo = 0.

Instruction lt

This instruction uses all constraints defined by instruction groups step_1, binary_operation, and keep_ram. Beyond that, this instruction has no transition constraints. Instead, correct transition is guaranteed by the U32 Table.

Instruction and

This instruction uses all constraints defined by instruction groups step_1, binary_operation, and keep_ram. Beyond that, this instruction has no transition constraints. Instead, correct transition is guaranteed by the U32 Table.

Instruction xor

This instruction uses all constraints defined by instruction groups step_1, binary_operation, and keep_ram. Beyond that, this instruction has no transition constraints. Instead, correct transition is guaranteed by the U32 Table.

Instruction log2floor

This instruction uses all constraints defined by instruction groups step_1, unary_operation, and keep_ram. Beyond that, this instruction has no transition constraints. Instead, correct transition is guaranteed by the U32 Table.

Instruction pow

This instruction uses all constraints defined by instruction groups step_1, binary_operation, and keep_ram. Beyond that, this instruction has no transition constraints. Instead, correct transition is guaranteed by the U32 Table.

Instruction div

This instruction uses all constraints defined by instruction groups step_1, stack_remains_and_top_3_unconstrained, and keep_ram. Additionally, it defines the following transition constraints.

Recall that instruction div takes stack _ d n and computes _ q r where n is the numerator, d is the denominator, r is the remainder, and q is the quotient. The following two properties are guaranteed by the U32 Table:

1. The remainder r is smaller than the denominator d, and
2. all four of n, d, q, and r are u32s.

Description

1. Numerator is quotient times denominator plus remainder: n == q·d + r.
2. Stack element st2 does not change.

Polynomials

1. st0 - st1·st1' - st0'
2. st2' - st2

Instruction pop_count

This instruction uses all constraints defined by instruction groups step_1, unary_operation, and keep_ram. Beyond that, this instruction has no transition constraints. Instead, correct transition is guaranteed by the U32 Table.

Instruction xxadd

This instruction uses all constraints defined by instruction groups step_1, stack_remains_and_top_3_unconstrained, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. The result of adding st0 to st3 is moved into st0.
2. The result of adding st1 to st4 is moved into st1.
3. The result of adding st2 to st5 is moved into st2.

Polynomials

1. st0' - (st0 + st3)
2. st1' - (st1 + st4)
3. st2' - (st2 + st5)

Instruction xxmul

This instruction uses all constraints defined by instruction groups step_1, stack_remains_and_top_3_unconstrained, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. The coefficient of x^0 of multiplying the two X-Field elements on the stack is moved into st0.
2. The coefficient of x^1 of multiplying the two X-Field elements on the stack is moved into st1.
3. The coefficient of x^2 of multiplying the two X-Field elements on the stack is moved into st2.

Polynomials

1. st0' - (st0·st3 - st2·st4 - st1·st5)
2. st1' - (st1·st3 + st0·st4 - st2·st5 + st2·st4 + st1·st5)
3. st2' - (st2·st3 + st1·st4 + st0·st5 + st2·st5)

Instruction xinvert

This instruction uses all constraints defined by instruction groups step_1, stack_remains_and_top_3_unconstrained, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. The coefficient of x^0 of multiplying X-Field element on top of the current stack and on top of the next stack is 1.
2. The coefficient of x^1 of multiplying X-Field element on top of the current stack and on top of the next stack is 0.
3. The coefficient of x^2 of multiplying X-Field element on top of the current stack and on top of the next stack is 0.

Polynomials

1. st0·st0' - st2·st1' - st1·st2' - 1
2. st1·st0' + st0·st1' - st2·st2' + st2·st1' + st1·st2'
3. st2·st0' + st1·st1' + st0·st2' + st2·st2'

Instruction xbmul

This instruction uses all constraints defined by instruction groups step_1, stack_shrinks_and_top_3_unconstrained, and keep_ram. Additionally, it defines the following transition constraints.

Description

1. The result of multiplying the top of the stack with the X-Field element's coefficient for x^0 is moved into st0.
2. The result of multiplying the top of the stack with the X-Field element's coefficient for x^1 is moved into st1.
3. The result of multiplying the top of the stack with the X-Field element's coefficient for x^2 is moved into st2.

Polynomials

1. st0' - st0·st1
2. st1' - st0·st2
3. st2' - st0·st3

Instruction read_io

This instruction uses all constraints defined by instruction groups step_1, grow_stack, and keep_ram. It has no additional transition constraints. An Evaluation Argument with the list of input symbols guarantees correct transition.

Instruction write_io

This instruction uses all constraints defined by instruction groups step_1, shrink_stack, and keep_ram. It has no additional transition constraints. An Evaluation Argument with the list of output symbols guarantees correct transition.

Operational Stack Table

The operational stack is where the program stores simple elementary operations, function arguments, and pointers to important objects. There are 16 registers (st0 through st15) that the program can access directly. These registers correspond to the top of the stack. They are recorded in the Processor Table.

The rest of the operational stack is stored in a dedicated memory object called “operational stack underflow memory”. It is initially empty. The evolution of the underflow memory is recorded in the Operational Stack Table.

Base Columns

The Operational Stack Table consists of 4 columns:

1. the cycle counter clk
2. the shrink stack indicator shrink_stack
3. the operational stack value osv, and
4. the operational stack pointer osp.

Columns clk, shrink_stack, osp, and osv correspond to columns clk, ib1, osp, and osv in the Processor Table, respectively. A Permutation Argument with the Processor Table establishes that, selecting the columns with these labels, the two tables' sets of rows are identical.

In order to guarantee memory consistency, the rows of the operational stack table are sorted by operational stack pointer osp first, cycle count clk second. The mechanics are best illustrated by an example. Observe how the malicious manipulation of the Op Stack Underflow Memory, the change of “42” into “99” in cycle 8, is detected: The transition constraints of the Op Stack Table stipulate that if osp does not change, then osv can only change if the shrink stack indicator shrink_stack is set. Consequently, row [5, push, 9, 42] being followed by row [_, _, 9, 99] violates the constraints. The shrink stack indicator being correct is guaranteed by the Permutation Argument between Op Stack Table and the Processor Table.

For illustrative purposes only, we use four stack registers st0 through st3 in the example. TritonVM has 16 stack registers, st0 through st15.

Execution trace:

Operational Stack Table:

Extension Columns

The Op Stack Table has 2 extension columns, rppa and ClockJumpDifferenceLookupClientLogDerivative.

1. A Permutation Argument establishes that the rows of the Op Stack Table correspond to the rows of the Processor Table. The running product for this argument is contained in the rppa column.
2. In order to achieve memory consistency, a Lookup Argument shows that all clock jump differences are contained in the clk column of the Processor Table. The logarithmic derivative for this argument is contained in the ClockJumpDifferenceLookupClientLogDerivative column.

Padding

A padding row is a direct copy of the Op Stack Table's row with the highest value for column clk, called template row, with the exception of the cycle count column clk. In a padding row, the value of column clk is 1 greater than the value of column clk in the template row. The padding row is inserted right below the template row. These steps are repeated until the desired padded height is reached. In total, above steps ensure that the Permutation Argument between the Op Stack Table and the Processor Table holds up.

Memory-Consistency

Memory-consistency follows from two more primitive properties:

1. Contiguity of regions of constant memory pointer. Since the memory pointer for the Op Stack table, osp can change by at most one per cycle, it is possible to enforce a full sorting using AIR constraints.
2. Correct inner-sorting within contiguous regions. Specifically, the rows within each contiguous region of constant memory pointer should be sorted for clock cycle. This property is established by the clock jump difference Lookup Argument. In a nutshell, every difference of consecutive clock cycles that occurs within one contiguous block of constant memory pointer is shown itself to be a valid clock cycle through a separate cross-table argument.

Arithmetic Intermediate Representation

Let all household items (🪥, 🛁, etc.) be challenges, concretely evaluation points, supplied by the verifier. Let all fruit & vegetables (🥝, 🥥, etc.) be challenges, concretely weights to compress rows, supplied by the verifier. Both types of challenges are X-field elements, i.e., elements of ${\mathbb{F}}_{p^3}$.

Initial Constraints

1. clk is 0
2. osv is 0.
3. osp is the number of available stack registers, i.e., 16.
4. The running product for the permutation argument with the Processor Table rppa starts off having accumulated the first row with respect to challenges 🍋, 🍊, 🍉, and 🫒 and indeterminate 🪤.
5. The logarithmic derivative for the clock jump difference lookup ClockJumpDifferenceLookupClientLogDerivative is 0.

Initial Constraints as Polynomials

1. clk
2. osv
3. osp - 16
4. rppa - (🪤 - 🍋·clk - 🍊·ib1 - 🍉·osp - 🫒osv)
5. ClockJumpDifferenceLookupClientLogDerivative

Consistency Constraints

None.

Transition Constraints

1. • the osp increases by 1, or
   • the osp does not change AND the osv does not change, or
   • the osp does not change AND the shrink stack indicator shrink_stack is 1.
2. The running product for the permutation argument with the Processor Table rppa absorbs the next row with respect to challenges 🍋, 🍊, 🍉, and 🫒 and indeterminate 🪤.
3. If the op stack pointer osp does not change, then the logarithmic derivative for the clock jump difference lookup ClockJumpDifferenceLookupClientLogDerivative accumulates a factor (clk' - clk) relative to indeterminate 🪞. Otherwise, it remains the same.

Written as Disjunctive Normal Form, the same constraints can be expressed as:

1. • the osp increases by 1 or the osp does not change
   • the osp increases by 1 or the osv does not change or the shrink stack indicator shrink_stack is 1
2. rppa' = rppa·(🪤 - 🍋·clk' - 🍊·ib1' - 🍉·osp' - 🫒osv')
3. • the osp changes or the logarithmic derivative accumulates a summand, and
   • the osp does not change or the logarithmic derivative does not change.

Transition Constraints as Polynomials

1. (osp' - (osp + 1))·(osp' - osp)
2. (osp' - (osp + 1))·(osv' - osv)·(1 - shrink_stack)
3. rppa' - rppa·(🪤 - 🍋·clk' - 🍊·ib1' - 🍉·osp' - 🫒osv')
4. (osp' - (osp + 1))·((ClockJumpDifferenceLookupClientLogDerivative' - ClockJumpDifferenceLookupClientLogDerivative) · (🪞 - clk' + clk) - 1)
+ (osp' - osp)·(ClockJumpDifferenceLookupClientLogDerivative' - ClockJumpDifferenceLookupClientLogDerivative)

Terminal Constraints

None.

Random Access Memory Table

The RAM is accessible through read_mem and write_mem commands.

Base Columns

The RAM Table has 7 columns:

1. the cycle counter clk,
2. the instruction executed in the previous clock cycle previous_instruction,
3. RAM address pointer ramp,
4. the value of the memory at that address ramv,
5. helper variable iord ("inverse of ramp difference", but elsewhere also "difference inverse" and di for short),
6. Bézout coefficient polynomial coefficient 0 bcpc0,
7. Bézout coefficient polynomial coefficient 1 bcpc1,

Columns clk, previous_instruction, ramp, and ramv correspond to the columns of the same name in the Processor Table. A permutation argument with the Processor Table establishes that, selecting the columns with these labels, the two tables' sets of rows are identical.

Column iord helps with detecting a change of ramp across two RAM Table rows. The function of iord is best explained in the context of sorting the RAM Table's rows, which is what the next section is about.

The Bézout coefficient polynomial coefficients bcpc0 and bcpc1 represent the coefficients of polynomials that are needed for the contiguity argument. This argument establishes that all regions of constant ramp are contiguous.

Extension Columns

The RAM Table has 2 extension columns, rppa and ClockJumpDifferenceLookupClientLogDerivative.

1. A Permutation Argument establishes that the rows in the RAM Table correspond to the rows of the Processor Table, after selecting for columns clk, ramp, ramv in both tables. The running product for this argument is contained in the rppa column.
2. In order to achieve memory consistency, a Lookup Argument shows that all clock jump differences are contained in the clk column of the Processor Table. The logarithmic derivative for this argument is contained in the ClockJumpDifferenceLookupClientLogDerivative column.

Sorting Rows

Up to order, the rows of the Hash Table in columns clk, ramp, ramv are identical to the rows in the Processor Table in columns clk, ramp, and ramv. In the Hash Table, the rows are arranged such that they

1. form contiguous regions of ramp, and
2. are sorted by cycle counter clk within each such region.

One way to achieve this is to sort by ramp first, clk second.

Coming back to iord: if the difference between ramp in row $i$ and row $i+1$ is 0, then iord in row $i$ is 0. Otherwise, iord in row $i$ is the multiplicative inverse of the difference between ramp in row $i+1$ and ramp in row $i$. In the last row, there being no next row, iord is 0.

An example of the mechanics can be found below. For reasons of display width, we abbreviate previous_instruction by pi. For illustrative purposes only, we use four stack registers st0 through st3 in the example. Triton VM has 16 stack registers, st0 through st15.

Processor Table:

RAM Table:

Padding

A padding row is a direct copy of the RAM Table's row with the highest value for column clk, called template row, with the exception of the cycle count column clk. In a padding row, the value of column clk is 1 greater than the value of column clk in the template row. The padding row is inserted right below the template row. Finally, the value of column iord is set to 0 in the template row. These steps are repeated until the desired padded height is reached. In total, above steps ensure that the Permutation Argument between the RAM Table and the Processor Table holds up.

Contiguity Argument

As a stepping stone to proving memory-consistency, it is necessary to prove that all regions of constant ramp are contiguous. In simpler terms, this condition stipulates that after filtering the rows in the RAM Table for any given ramp value, the resulting sublist of rows forms a contiguous sublist with no gaps. The contiguity establishes this property. What follows here is a summary of the Contiguity Argument for RAM Consistency.

The contiguity argument is a Randomized AIR without Preprocessing (RAP). In particular, there are 4 extension columns whose values depend on the verifier's challenge $\alpha$:

• The running product polynomial rpp, which accumulates a factor $(\alpha -\mathsf{ramp})$ in every consecutive pair of rows (including the first) where the current row's ramp value is different from the previous row's ramp value.
• The formal derivative fd, which is updated according to the product rule of differentiation and therefore tracks the formal derivative of rpp.
• The Bézout coefficient 0 bc0, which is the evaluation of the polynomial defined by the coefficients of bcpc0 in $\alpha$.
• The Bézout coefficient 1 bc1, which is the evaluation of the polynomial defined by the coefficients of bcpc1 in $\alpha$.

The contiguity of regions of constant ramp is implied by the square-freeness (as a polynomial in $\alpha$) of rpp. If rpp is square-free, then the Bézout relation

$$bc0\cdot \mathsf{rpp}+bc1\cdot \mathsf{fd}=1$$

holds for any $\alpha$. However, if rp is not square-free, indicating a malicious prover, then the above relation holds in a negligible fraction of possible $\alpha$'s. Therefore, the AIR enforces the Bézout relation as a terminal boundary constraint.

Inner Sorting

The second stepping stone to proving memory-consistency is to establish that the rows in each region of constant ramp are correctly sorted for clk in ascending order. To prove this property, we show that all differences of clk values difference greater than 1 in consecutive rows with the same ramp value – the clock jump differences – are contained in the clk table of the Processor Table. What follows here is a summary of the construction reduced to the RAM Table; the bulk of the logic and constraints that make this argument work is located in the Processor Table. The entirety of this construction is motivated and explained in TIP-0003.

The inner sorting argument requires one extension column cjdrp, which contains a running product. Specifically, this column accumulates a factor $\beta -({\mathsf{clk}}^{\prime }-\mathsf{clk})$ in every pair of consecutive rows where a) the ramp value is the same, and b) the difference in clk values minus one is different from zero.

Row Permutation Argument

Selecting for the columns clk, ramp, and ramv, the set of rows of the RAM Table is identical to the set of rows of the Processor Table. This argument requires one extension column, rppa, short for "running product for Permutation Argument". This column accumulates a factor $(a\cdot \mathsf{clk}+b\cdot \mathsf{ramp}+c\cdot \mathsf{ramv}-\gamma )$ in every row. In this expression, $a$, $b$, $c$, and $\gamma$ are challenges from the verifier.

Arithmetic Intermediate Representation

Let all household items (🪥, 🛁, etc.) be challenges, concretely evaluation points, supplied by the verifier. Let all fruit & vegetables (🥝, 🥥, etc.) be challenges, concretely weights to compress rows, supplied by the verifier. Both types of challenges are X-field elements, i.e., elements of ${\mathbb{F}}_{p^3}$.

Initial Constraints

1. The first coefficient of the Bézout coefficient polynomial 0 bcpc0 is 0.
2. The Bézout coefficient 0 bc0 is 0.
3. The Bézout coefficient 1 bc1 is equal to the first coefficient of the Bézout coefficient polynomial bcpc1.
4. The running product polynomial rpp starts with 🧼 - ramp.
5. The formal derivative fd starts with 1.
6. The running product for the permutation argument with the Processor Table rppa has absorbed the first row with respect to challenges 🍍, 🍈, 🍎, and 🌽 and indeterminate 🛋.
7. The logarithmic derivative for the clock jump difference lookup ClockJumpDifferenceLookupClientLogDerivative is 0.

Initial Constraints as Polynomials

1. bcpc0
2. bc0
3. bc1 - bcpc1
4. rpp - 🧼 + ramp
5. fd - 1
6. rppa - 🛋 - 🍍·clk - 🍈·ramp - 🍎·ramv - 🌽·previous_instruction
7. ClockJumpDifferenceLookupClientLogDerivative

Consistency Constraints

None.

Transition Constraints

1. If (ramp - ramp') is 0, then iord is 0, else iord is the multiplicative inverse of (ramp' - ramp).
2. If the ramp does not change and previous_instruction in the next row is not write_mem, then the RAM value ramv does not change.
3. The Bézout coefficient polynomial coefficients are allowed to change only when the ramp changes.
4. The running product polynomial rpp accumulates a factor (🧼 - ramp) whenever ramp changes.
5. The running product for the permutation argument with the Processor Table rppa absorbs the next row with respect to challenges 🍍, 🍈, 🍎, and 🌽 and indeterminate 🛋.
6. If the RAM pointer ramp does not change, then the logarithmic derivative for the clock jump difference lookup ClockJumpDifferenceLookupClientLogDerivative accumulates a factor (clk' - clk) relative to indeterminate 🪞. Otherwise, it remains the same.

Written as Disjunctive Normal Form, the same constraints can be expressed as:

1. iord is 0 or iord is the inverse of (ramp' - ramp).
2. (ramp' - ramp) is zero or iord is the inverse of (ramp' - ramp).
3. (ramp' - ramp) non-zero or previous_instruction' is opcode(write_mem) or ramv' is ramv.
4. bcpc0' - bcpc0 is zero or (ramp' - ramp) is nonzero.
5. bcpc1' - bcpc1 is zero or (ramp' - ramp) is nonzero.
6. (ramp' - ramp) is zero and rpp' = rpp; or (ramp' - ramp) is nonzero and rpp' = rpp·(ramp'-🧼)) is zero.
7. the formal derivative fd applies the product rule of differentiation (as necessary).
8. Bézout coefficient 0 is evaluated correctly.
9. Bézout coefficient 1 is evaluated correctly.
10. rppa' = rppa·(🛋 - 🍍·clk' - 🍈·ramp' - 🍎·ramv' - 🌽·previous_instruction')
11. • the ramp changes or the logarithmic derivative accumulates a summand, and
    • the ramp does not change or the logarithmic derivative does not change.

Transition Constraints as Polynomials

1. iord·(iord·(ramp' - ramp) - 1)
2. (ramp' - ramp)·(iord·(ramp' - ramp) - 1)
3. (1 - iord·(ramp' - ramp))·(previous_instruction - opcode(write_mem))·(ramv' - ramv)
4. (iord·(ramp' - ramp) - 1)·(bcpc0' - bcpc0)
5. (iord·(ramp' - ramp) - 1)·(bcpc1' - bcpc1)
6. (iord·(ramp' - ramp) - 1)·(rpp' - rpp) + (ramp' - ramp)·(rpp' - rpp·(ramp'-🧼))
7. (iord·(ramp' - ramp) - 1)·(fd' - fd) + (ramp' - ramp)·(fd' - fd·(ramp'-🧼) - rpp)
8. (iord·(ramp' - ramp) - 1)·(bc0' - bc0) + (ramp' - ramp)·(bc0' - bc0·🧼 - bcpc0')
9. (iord·(ramp' - ramp) - 1)·(bc1' - bc1) + (ramp' - ramp)·(bc1' - bc1·🧼 - bcpc1')
10. rppa' - rppa·(🛋 - 🍍·clk' - 🍈·ramp' - 🍎·ramv' - 🌽·previous_instruction')
11. (iord·(ramp' - ramp) - 1)·((ClockJumpDifferenceLookupClientLogDerivative' - ClockJumpDifferenceLookupClientLogDerivative) · (🪞 - clk' + clk) - 1)
+ (ramp' - ramp)·(ClockJumpDifferenceLookupClientLogDerivative' - ClockJumpDifferenceLookupClientLogDerivative)

Terminal Constraints

1. The Bézout relation holds between rp, fd, bc0, and bc1.

Terminal Constraints as Polynomials

1. rpp·bc0 + fd·bc1 - 1

Jump Stack Table

The Jump Stack Memory contains the underflow from the Jump Stack.

Base Columns

The Jump Stack Table consists of 5 columns:

1. the cycle counter clk
2. current instruction ci,
3. the jump stack pointer jsp,
4. the last jump's origin jso, and
5. the last jump's destination jsd.

The rows are sorted by jump stack pointer jsp, then by cycle counter clk. The column jsd contains the destination of stack-extending jump (call) as well as of the no-stack-change jump (recurse); the column jso contains the source of the stack-extending jump (call) or equivalently the destination of the stack-shrinking jump (return).

The AIR for this table guarantees that the return address of a single cell of return address memory can change only if there was a call instruction.

An example program, execution trace, and jump stack table are shown below.

Program:

Execution trace:

Jump Stack Table:

Extension Columns

The Jump Stack Table has 2 extension columns, rppa and ClockJumpDifferenceLookupClientLogDerivative.

1. A Permutation Argument establishes that the rows of the Jump Stack Table match with the rows in the Processor Table. The running product for this argument is contained in the rppa column.
2. In order to achieve memory consistency, a Lookup Argument shows that all clock jump differences are contained in the clk column of the Processor Table. The logarithmic derivative for this argument is contained in the ClockJumpDifferenceLookupClientLogDerivative column.

Padding

A padding row is a direct copy of the Jump Stack Table's row with the highest value for column clk, called template row, with the exception of the cycle count column clk. In a padding row, the value of column clk is 1 greater than the value of column clk in the template row. The padding row is inserted right below the template row. These steps are repeated until the desired padded height is reached. In total, above steps ensure that the Permutation Argument between the Jump Stack Table and the Processor Table holds up.

Memory-Consistency

Memory-consistency follows from two more primitive properties:

1. Contiguity of regions of constant memory pointer. Since the memory pointer for the JumpStack table, jsp can change by at most one per cycle, it is possible to enforce a full sorting using AIR constraints.
2. Correct inner-sorting within contiguous regions. Specifically, the rows within each contiguous region of constant memory pointer should be sorted for clock cycle. This property is established by the clock jump difference Lookup Argument. In a nutshell, every difference of consecutive clock cycles that occurs within one contiguous block of constant memory pointer is shown itself to be a valid clock cycle through a separate cross-table argument.

Arithmetic Intermediate Representation

Let all household items (🪥, 🛁, etc.) be challenges, concretely evaluation points, supplied by the verifier. Let all fruit & vegetables (🥝, 🥥, etc.) be challenges, concretely weights to compress rows, supplied by the verifier. Both types of challenges are X-field elements, i.e., elements of ${\mathbb{F}}_{p^3}$.

Initial Constraints

1. Cycle count clk is 0.
2. Jump Stack Pointer jsp is 0.
3. Jump Stack Origin jso is 0.
4. Jump Stack Destination jsd is 0.
5. The running product for the permutation argument with the Processor Table rppa has absorbed the first row with respect to challenges 🍇, 🍅, 🍌, 🍏, and 🍐 and indeterminate 🧴.
6. The running product of clock jump differences ClockJumpDifferenceLookupClientLogDerivative is 0.

Initial Constraints as Polynomials

1. clk
2. jsp
3. jso
4. jsd
5. rppa - (🧴 - 🍇·clk - 🍅·ci - 🍌·jsp - 🍏·jso - 🍐·jsd)
6. ClockJumpDifferenceLookupClientLogDerivative

Consistency Constraints

None.

Transition Constraints

1. The jump stack pointer jsp increases by 1, or
2. (jsp does not change and jso does not change and jsd does not change and the cycle counter clk increases by 1), or
3. (jsp does not change and jso does not change and jsd does not change and the current instruction ci is call), or
4. (jsp does not change and the current instruction ci is return).
5. The running product for the permutation argument rppa absorbs the next row with respect to challenges 🍇, 🍅, 🍌, 🍏, and 🍐 and indeterminate 🧴.
6. If the jump stack pointer jsp does not change, then the logarithmic derivative for the clock jump difference lookup ClockJumpDifferenceLookupClientLogDerivative accumulates a factor (clk' - clk) relative to indeterminate 🪞. Otherwise, it remains the same.

Written as Disjunctive Normal Form, the same constraints can be expressed as:

1. The jump stack pointer jsp increases by 1 or the jump stack pointer jsp does not change
2. The jump stack pointer jsp increases by 1 or the jump stack origin jso does not change or current instruction ci is return
3. The jump stack pointer jsp increases by 1 or the jump stack destination jsd does not change or current instruction ci is return
4. The jump stack pointer jsp increases by 1 or the cycle count clk increases by 1 or current instruction ci is call or current instruction ci is return
5. rppa' - rppa·(🧴 - 🍇·clk' - 🍅·ci' - 🍌·jsp' - 🍏·jso' - 🍐·jsd')
6. • the jsp changes or the logarithmic derivative accumulates a summand, and
   • the jsp does not change or the logarithmic derivative does not change.

Transition Constraints as Polynomials

1. (jsp' - (jsp + 1))·(jsp' - jsp)
2. (jsp' - (jsp + 1))·(jso' - jso)·(ci - op_code(return))
3. (jsp' - (jsp + 1))·(jsd' - jsd)·(ci - op_code(return))
4. (jsp' - (jsp + 1))·(clk' - (clk + 1))·(ci - op_code(call))·(ci - op_code(return))
5. clk_di·(jsp' - jsp - 1)·(1 - clk_di·(clk' - clk - one))
6. (clk' - clk - one)·(jsp' - jsp - 1)·(1 - clk_di·(clk' - clk - one))
7. rppa' - rppa·(🧴 - 🍇·clk' - 🍅·ci' - 🍌·jsp' - 🍏·jso' - 🍐·jsd')
8. (jsp' - (jsp + 1))·((ClockJumpDifferenceLookupClientLogDerivative' - ClockJumpDifferenceLookupClientLogDerivative) · (🪞 - clk' + clk) - 1)
+ (jsp' - jsp)·(ClockJumpDifferenceLookupClientLogDerivative' - ClockJumpDifferenceLookupClientLogDerivative)

Terminal Constraints

None.

Hash Table

The instruction hash hashes the OpStack's 10 top-most elements in one cycle. Similarly, the Sponge instructions absorb_init, absorb, and squeeze also all complete in one cycle. The main processor achieves this by using a hash coprocessor. The Hash Table is part of the arithmetization of that coprocessor, the other two parts being the Cascade Table and the Lookup Table. In addition to accelerating these hashing instructions, the Hash Table helps with program attestation by hashing the program.

The arithmetization for instruction hash, the Sponge instructions absorb_init, absorb, and squeeze, and for program hashing are quite similar. The main differences are in updates to the state registers between executions of the pseudo-random permutation used in Triton VM, the permutation of Tip5. A summary of the four instructions' mechanics:

• Instruction hash
  1. sets all the hash coprocessor's rate registers (state_0 through state_9) to equal the processor's stack registers state_0 through state_9,
  2. sets all the hash coprocessor's capacity registers (state_10 through state_15) to 1,
  3. executes the 5 rounds of the Tip5 permutation,
  4. overwrites the processor's stack registers state_0 through state_4 with 0, and
  5. overwrites the processor's stack registers state_5 through state_9 with the hash coprocessor's registers state_0 through state_4.
• Instruction absorb_init
  1. sets all the hash coprocessor's rate registers (state_0 through state_9) to equal the processor's stack registers state_0 through state_9,
  2. sets all the hash coprocessor's capacity registers (state_10 through state_15) to 0, and
  3. executes the 5 rounds of the Tip5 permutation.
• Instruction absorb
  1. overwrites the hash coprocessor's rate registers (state_0 through state_9) with the processor's stack registers state_0 through state_9, and
  2. executes the 5 rounds of the Tip5 permutation.
• Instruction squeeze
  1. overwrites the processor's stack registers state_0 through state_9 with the hash coprocessor's rate registers (state_0 through state_9), and
  2. executes the 5 rounds of the Tip5 permutation.

Program hashing happens in the initialization phase of Triton VM. The to-be-executed program has no control over it. Program hashing is mechanically identical to performing instruction absorb as often as is necessary to hash the entire program. A notable difference is the source of the to-be-absorbed elements: they come from program memory, not the processor (which is not running yet). Once all instructions have been absorbed, the resulting digest is checked against the publicly claimed digest.

Due to the various similar but distinct tasks of the Hash Table, it has an explicit Mode register. The four separate modes are program_hashing, sponge, hash, and pad, and they evolve in that order. Changing the mode is only possible when the permutation has been applied in full, i.e., when the round number is 5. Once mode pad is reached, it is not possible to change the mode anymore. It is not possible to skip mode program_hashing: the program is always hashed. Skipping any or all of the modes sponge, hash, or pad is possible in principle:

• if no Sponge instructions are executed, mode sponge will be skipped,
• if no hash instruction is executed, mode hash will be skipped, and
• if the Hash Table does not require any padding, mode pad will be skipped.

The distinct modes translate into distinct sections in the Hash Table, which are recorded in order: First, the entire Sponge's transition of hashing the program is recorded. Then, the Hash Table records all Sponge instructions in the order the processor executed them. Then, the Hash Table records all hash instructions in the order the processor executed them. Lastly, as many padding rows as necessary are inserted. In total, this separation allows the processor to execute hash instructions without affecting the Sponge's state, and keeps program hashing independent from both.

Note that state_0 through state_3, corresponding to those states that are being split-and-looked-up in the Tip5 permutation, are not stored as a single field element. Instead, four limbs “highest”, “mid high”, “mid low”, and “lowest” are recorded in the Hash Table. This (basically) corresponds to storing the result of $\sigma (R\cdot \text{state\_element})$. In the Hash Table, the resulting limbs are 16 bit wide, and hence, there are only 4 limbs; the split into 8-bit limbs happens in the Cascade Table. For convenience, this document occasionally refers to those states as if they were a single register. This is an alias for $(2^{48}\cdot \text{state\_i\_highest\_lkin}+2^{32}\cdot \text{state\_i\_mid\_high\_lkin}+2^{16}\cdot \text{state\_i\_mid\_low\_lkin}+\text{state\_i\_lowest\_lkin})\cdot R^{-1}$.

Base Columns

The Hash Table has 67 base columns:

• The Mode indicator, as described above. It takes value
  • $1$ for mode program_hashing,
  • $2$ for mode sponge,
  • $3$ for mode hash, and
  • $0$ for mode pad.
• Current instruction CI, holding the instruction the processor is currently executing. This column is only relevant for mode sponge.
• Round number indicator round_no, which can be one of $\{0,\dots ,5\}$. The Tip5 permutation has 5 rounds, indexed $\{0,\dots ,4\}$. The round number 5 indicates that the Tip5 permutation has been applied in full.
• 16 columns state_i_highest_lkin, state_i_mid_high_lkin, state_i_mid_low_lkin, state_i_lowest_lkin for the to-be-looked-up value of state_0 through state_4, each of which holds one 16-bit wide limb.
• 16 columns state_i_highest_lkout, state_i_mid_high_lkout, state_i_mid_low_lkout, state_i_lowest_lkout for the looked-up value of state_0 through state_4, each of which holds one 16-bit wide limb.
• 12 columns state_5 through state_15.
• 4 columns state_i_inv establishing correct decomposition of state_0_*_lkin through state_3_*_lkin into 16-bit wide limbs.
• 16 columns constant_i, which hold the round constant for the round indicated by RoundNumber, or 0 if no round with this round number exists.

Extension Columns

The Hash Table has 20 extension columns:

• RunningEvaluationReceiveChunk for the Evaluation Argument for copying chunks of size $\text{rate}$ from the Program Table. Relevant for program attestation.
• RunningEvaluationHashInput for the Evaluation Argument for copying the input to the hash function from the processor to the hash coprocessor,
• RunningEvaluationHashDigest for the Evaluation Argument for copying the hash digest from the hash coprocessor to the processor,
• RunningEvaluationSponge for the Evaluation Argument for copying the 10 next to-be-absorbed elements from the processor to the hash coprocessor or the 10 next squeezed elements from the hash coprocessor to the processor, depending on the instruction,
• 16 columns state_i_limb_LookupClientLogDerivative (for i $\in \{0,\dots ,3\}$ and limb $\in \{$highest, mid_high, mid_low, lowest $\}$) establishing correct lookup of the respective limbs in the Cascade Table.

Padding

Each padding row is the all-zero row with the exception of

• CI, which is the opcode of instruction hash,
• state_i_inv for i $\in \{0,\dots ,3\}$, which is $(2^{32}-1{)}^{-1}$, and
• constant_i for i $\in \{0,\dots ,15\}$, which is the ith constant for round 0.

Arithmetic Intermediate Representation

Let all household items (🪥, 🛁, etc.) be challenges, concretely evaluation points, supplied by the verifier. Let all fruit & vegetables (🥝, 🥥, etc.) be challenges, concretely weights to compress rows, supplied by the verifier. Both types of challenges are X-field elements, i.e., elements of ${\mathbb{F}}_{p^3}$.

Initial Constraints

1. The Mode is program_hashing.
2. The round number is 0.
3. RunningEvaluationReceiveChunk has absorbed the first chunk of instructions with respect to indeterminate 🪣.
4. RunningEvaluationHashInput is 1.
5. RunningEvaluationHashDigest is 1.
6. RunningEvaluationSponge is 1.
7. For i $\in \{0,\dots ,3\}$ and limb $\in \{$highest, mid_high, mid_low, lowest $\}$:
   state_i_limb_LookupClientLogDerivative has accumulated state_i_limb_lkin and state_i_limb_lkout with respect to challenges 🍒, 🍓 and indeterminate 🧺.

Initial Constraints as Polynomials

1. Mode - 1
2. round_no
3. RunningEvaluationReceiveChunk - 🪣 - (🪑^10 + state_0·🪑^9 + state_1·🪑^8 + state_2·🪑^7 + state_3·🪑^6 + state_4·🪑^5 + state_5·🪑^4 + state_6·🪑^3 + state_7·🪑^2 + state_8·🪑 + state_9)
4. RunningEvaluationHashInput - 1
5. RunningEvaluationHashDigest - 1
6. RunningEvaluationSponge - 1
7. For i $\in \{0,\dots ,3\}$ and limb $\in \{$highest, mid_high, mid_low, lowest $\}$:
   state_i_limb_LookupClientLogDerivative·(🧺 - 🍒·state_i_limb_lkin - 🍓·state_i_limb_lkout) - 1

Consistency Constraints

1. The Mode is a valid mode, i.e., $\in \{0,\dots ,3\}$.
2. If the Mode is program_hashing, hash, or pad, then the current instruction is the opcode of hash.
3. If the Mode is sponge, then the current instruction is a Sponge instruction.
4. If the Mode is pad, then the round_no is 0.
5. For i $\in \{10,\dots ,15\}$: If the round number is 0 and the current Mode is hash, then register state_i is 1.
6. For i $\in \{10,\dots ,15\}$: If the round number is 0 and the current instruction is absorb_init, then register state_i is 0.
7. For i $\in \{0,\dots ,3\}$: ensure that decomposition of state_i is unique. That is, if both high limbs of state_i are the maximum value, then both low limbs are 0¹. To make the corresponding polynomials low degree, register state_i_inv holds the inverse-or-zero of the re-composed highest two limbs of state_i subtracted from their maximum value. Let state_i_hi_limbs_minus_2_pow_32 be an alias for that difference: state_i_hi_limbs_minus_2_pow_32 $:=2^{32}-1-2^{16}\cdot$state_i_highest_lk_in$-$state_i_mid_high_lk_in.
   1. If the two high limbs of state_i are both the maximum possible value, then the two low limbs of state_i are both 0.
   2. The state_i_inv is the inverse of state_i_hi_limbs_minus_2_pow_32 or state_i_inv is 0.
   3. The state_i_inv is the inverse of state_i_hi_limbs_minus_2_pow_32 or state_i_hi_limbs_minus_2_pow_32 is 0.
8. The round constants adhere to the specification of Tip5.

Consistency Constraints as Polynomials

1. (Mode - 0)·(Mode - 1)·(Mode - 2)·(Mode - 3)
2. (Mode - 2)·(CI - opcode(hash))
3. (Mode - 0)·(Mode - 1)·(Mode - 3)
·(CI - opcode(absorb_init))·(CI - opcode(absorb))·(CI - opcode(squeeze))
4. (Mode - 1)·(Mode - 2)·(Mode - 3)·(round_no - 0)
5. For i $\in \{10,\dots ,15\}$:
   (round_no - 1)·(round_no - 2)·(round_no - 3)·(round_no - 4)·(round_no - 5)
·(Mode - 0)·(Mode - 1)·(Mode - 2)
·(state_i - 1)
6. For i $\in \{10,\dots ,15\}$:
   (round_no - 1)·(round_no - 2)·(round_no - 3)·(round_no - 4)·(round_no - 5)
·(CI - opcode(hash))·(CI - opcode(absorb))·(CI - opcode(squeeze))
·(state_i - 0)
7. For i $\in \{0,\dots ,3\}$: define state_i_hi_limbs_minus_2_pow_32 := 2^32 - 1 - 2^16·state_i_highest_lk_in - state_i_mid_high_lk_in.
   1. (1 - state_i_inv · state_i_hi_limbs_minus_2_pow_32)·(2^16·state_i_mid_low_lk_in + state_i_lowest_lk_in)
   2. (1 - state_i_inv · state_i_hi_limbs_minus_2_pow_32)·state_i_inv
   3. (1 - state_i_inv · state_i_hi_limbs_minus_2_pow_32)·state_i_hi_limbs_minus_2_pow_32

Transition Constraints

1. If the round_no is 5, then the round_no in the next row is 0.
2. If the Mode is not pad and the round_no is not 5, then the round_no increments by 1.
3. If the Mode in the next row is program_hashing and the round_no in the next row is 0, then receive a chunk of instructions with respect to challenges 🪣 and 🪑.
4. If the Mode changes from program_hashing, then the Evaluation Argument of state_0 through state_4 with respect to indeterminate 🥬 equals the public program digest challenge, 🫑.
5. If the Mode is program_hashing and the Mode in the next row is sponge, then the current instructions in the next row is absorb_init.
6. If the round_no is not 5, then the current instruction does not change.
7. If the round_no is not 5, then the Mode does not change.
8. If the Mode is sponge, then the Mode in the next row is sponge or hash or pad.
9. If the Mode is hash, then the Mode in the next row is hash or pad.
10. If the Mode is pad, then the Mode in the next row is pad.
11. If the round_no in the next row is 0 and either (a) the Mode in the next row is program_hashing or (b) the Mode in the next row is sponge and the current instruction in the next row is absorb, then the capacity's state registers don't change.
12. If the round_no in the next row is 0 and the current instruction in the next row is squeeze, then none of the state registers change.
13. If the round_no in the next row is 0 and the Mode in the next row is hash, then RunningEvaluationHashInput accumulates the next row with respect to challenges 🧄₀ through 🧄₉ and indeterminate 🚪. Otherwise, it remains unchanged.
14. If the round_no in the next row is 5 and the Mode in the next row is hash, then RunningEvaluationHashDigest accumulates the next row with respect to challenges 🧄₀ through 🧄₄ and indeterminate 🪟. Otherwise, it remains unchanged.
15. If the round_no in the next row is 0 and the Mode in the next row is sponge, then RunningEvaluationSponge accumulates the next row with respect to challenges 🧅 and 🧄₀ through 🧄₉ and indeterminate 🧽. Otherwise, it remains unchanged.
16. For i $\in \{0,\dots ,3\}$ and limb $\in \{$highest, mid_high, mid_low, lowest $\}$:
    If the next round number is not 5, then state_i_limb_LookupClientLogDerivative has accumulated state_i_limb_lkin' and state_i_limb_lkout' with respect to challenges 🍒, 🍓 and indeterminate 🧺. Otherwise, state_i_limb_LookupClientLogDerivative remains unchanged.
17. For r $\in \{0,\dots ,4\}$:
    If the round_no is r, the state registers adhere to the rules of applying round r of the Tip5 permutation.

Transition Constraints as Polynomials

1. (round_no - 0)·(round_no - 1)·(round_no - 2)·(round_no - 3)·(round_no - 4)·(round_no' - 0)
2. (Mode - 0)·(round_no - 5)·(round_no' - round_no - 1)
3. RunningEvaluationReceiveChunk' - 🪣·RunningEvaluationReceiveChunk - (🪑^10 + state_0·🪑^9 + state_1·🪑^8 + state_2·🪑^7 + state_3·🪑^6 + state_4·🪑^5 + state_5·🪑^4 + state_6·🪑^3 + state_7·🪑^2 + state_8·🪑 + state_9)
4. (Mode - 0)·(Mode - 2)·(Mode - 3)·(Mode' - 1)·(🥬^5 + state_0·🥬^4 + state_1·🥬^3 + state_2·🥬^2 + state_3·🥬^1 + state_4 - 🫑)
5. (Mode - 0)·(Mode - 2)·(Mode - 3)·(Mode' - 2)·(CI' - opcode(absorb_init))
6. (round_no - 5)·(CI' - CI)
7. (round_no - 5)·(Mode' - Mode)
8. (Mode - 0)·(Mode - 1)·(Mode - 3)·(Mode' - 0)·(Mode' - 2)·(Mode' - 3)
9. (Mode - 0)·(Mode - 1)·(Mode - 2)·(Mode' - 0)·(Mode' - 3)
10. (Mode - 1)·(Mode - 2)·(Mode - 3)·(Mode' - 0)
11. (round_no - 1)·(round_no - 2)·(round_no - 3)·(round_no - 4)·(round_no - 5)
·(Mode' - 0)·(Mode' - 3)·(CI' - opcode(hash))·(CI' - opcode(absorb_init))·(CI' - opcode(squeeze))
·(🧄₁₀·(state_10' - state_10) + 🧄₁₁·(state_11' - state_11) + 🧄₁₂·(state_12' - state_12) + 🧄₁₃·(state_13' - state_13) + 🧄₁₄·(state_14' - state_14) + 🧄₁₅·(state_15' - state_15))
12. (round_no' - 1)·(round_no' - 2)·(round_no' - 3)·(round_no' - 4)·(round_no' - 5)
·(CI' - opcode(hash))·(CI' - opcode(absorb_init))·(CI' - opcode(absorb))
·(🧄₀·(state_0' - state_0) + 🧄₁·(state_1' - state_1) + 🧄₂·(state_2' - state_2) + 🧄₃·(state_3' - state_3) + 🧄₄·(state_4' - state_4)
+ 🧄₅·(state_5' - state_5) + 🧄₆·(state_6' - state_6) + 🧄₇·(state_7' - state_7) + 🧄₈·(state_8' - state_8) + 🧄₉·(state_9' - state_9)
+ 🧄₁₀·(state_10' - state_10) + 🧄₁₁·(state_11' - state_11) + 🧄₁₂·(state_12' - state_12) + 🧄₁₃·(state_13' - state_13) + 🧄₁₄·(state_14' - state_14) + 🧄₁₅·(state_15' - state_15))
13. (round_no' - 0)·(round_no' - 1)·(round_no' - 2)·(round_no' - 3)·(round_no' - 4)
·(RunningEvaluationHashInput' - 🚪·RunningEvaluationHashInput - 🧄₀·state_0' - 🧄₁·state_1' - 🧄₂·state_2' - 🧄₃·state_3' - 🧄₄·state_4' - 🧄₅·state_5' - 🧄₆·state_6' - 🧄₇·state_7' - 🧄₈·state_8' - 🧄₉·state_9')
+ (round_no' - 0)·(RunningEvaluationHashInput' - RunningEvaluationHashInput)
+ (Mode' - 3)·(RunningEvaluationHashInput' - RunningEvaluationHashInput)
14. (round_no' - 0)·(round_no' - 1)·(round_no' - 2)·(round_no' - 3)·(round_no' - 4)
·(Mode' - 0)·(Mode' - 1)·(Mode' - 2)
·(RunningEvaluationHashDigest' - 🪟·RunningEvaluationHashDigest - 🧄₀·state_0' - 🧄₁·state_1' - 🧄₂·state_2' - 🧄₃·state_3' - 🧄₄·state_4')
+ (round_no' - 5)·(RunningEvaluationHashDigest' - RunningEvaluationHashDigest)
+ (Mode' - 3)·(RunningEvaluationHashDigest' - RunningEvaluationHashDigest)
15. (round_no' - 1)·(round_no' - 2)·(round_no' - 3)·(round_no' - 4)·(round_no' - 5)
·(CI' - opcode(hash))
·(RunningEvaluationSponge' - 🧽·RunningEvaluationSponge - 🧅·CI' - 🧄₀·state_0' - 🧄₁·state_1' - 🧄₂·state_2' - 🧄₃·state_3' - 🧄₄·state_4' - 🧄₅·state_5' - 🧄₆·state_6' - 🧄₇·state_7' - 🧄₈·state_8' - 🧄₉·state_9')
+ (RunningEvaluationSponge' - RunningEvaluationSponge)·(round_no' - 0)
+ (RunningEvaluationSponge' - RunningEvaluationSponge)·(CI' - opcode(absorb_init))·(CI' - opcode(absorb))·(CI' - opcode(squeeze))
16. For i $\in \{0,\dots ,3\}$ and limb $\in \{$highest, mid_high, mid_low, lowest $\}$:
    (round_no - 5)·((state_i_limb_LookupClientLogDerivative' - state_i_limb_LookupClientLogDerivative)·(🧺 - 🍒·state_i_limb_lkin' - 🍓·state_i_limb_lkout') - 1)
+ (round_no - 0)·(round_no - 1)·(round_no - 2)·(round_no - 3)·(round_no - 4)·(state_i_limb_LookupClientLogDerivative' - state_i_limb_LookupClientLogDerivative)
17. The remaining constraints are left as an exercise to the reader. For hints, see the Tip5 paper.

Terminal Constraints

1. If the Mode is program_hashing, then the Evaluation Argument of state_0 through state_4 with respect to indeterminate 🥬 equals the public program digest challenge, 🫑.
2. If the Mode is not pad, then the round_no is 5.

Terminal Constraints as Polynomials

1. 🥬^5 + state_0·🥬^4 + state_1·🥬^3 + state_2·🥬^2 + state_3·🥬 + state_4 - 🫑
2. (Mode - 0)·(round_no - 5)

Cascade Table

The Cascade Table helps arithmetizing the lookups necessary for the split-and-lookup S-box used in the Tip5 permutation. The main idea is to allow the Hash Table to look up limbs that are 16 bit wide even though the S-box is defined over limbs that are 8 bit wide. The Cascade Table facilitates the translation of limb widths. For the actual lookup of the 8-bit limbs, the Lookup Table is used. For a more detailed explanation and in-depth analysis, see the Tip5 paper.

Base Columns

The Cascade Table has 6 base columns:

Extension Columns

The Cascade Table has 2 extension columns:

• HashTableServerLogDerivative, the (running sum of the) logarithmic derivative for the Lookup Argument with the Hash Table. In every row, the sum accumulates LookupMultiplicity / (🧺 - Combo) where 🧺 is a verifier-supplied challenge and Combo is the weighted sum of LookInHi · 2^8 + LookInLo and LookOutHi · 2^8 + LookOutLo with weights 🍒 and 🍓 supplied by the verifier.
• LookupTableClientLogDerivative, the (running sum of the) logarithmic derivative for the Lookup Argument with the Lookup Table. In every row, the sum accumulates the two summands
  1. 1 / combo_hi where combo_hi is the verifier-weighted combination of LookInHi and LookOutHi, and
  2. 1 / combo_lo where combo_lo is the verifier-weighted combination of LookInLo and LookOutLo.

Padding

Each padding row is the all-zero row with the exception of IsPadding, which is 1.

Arithmetic Intermediate Representation

Let all household items (🪥, 🛁, etc.) be challenges, concretely evaluation points, supplied by the verifier. Let all fruit & vegetables (🥝, 🥥, etc.) be challenges, concretely weights to compress rows, supplied by the verifier. Both types of challenges are X-field elements, i.e., elements of ${\mathbb{F}}_{p^3}$.

Initial Constraints

1. If the first row is not a padding row, then HashTableServerLogDerivative has accumulated the first row with respect to challenges 🍒 and 🍓 and indeterminate 🧺. Else, HashTableServerLogDerivative is 0.
2. If the first row is not a padding row, then LookupTableClientLogDerivative has accumulated the first row with respect to challenges 🥦 and 🥒 and indeterminate 🪒. Else, LookupTableClientLogDerivative is 0.

Initial Constraints as Polynomials

1. (1 - IsPadding)·(HashTableServerLogDerivative·(🧺 - 🍒·(2^8·LookInHi + LookInLo) - 🍓·(2^8 · LookOutHi + LookOutLo)) - LookupMultiplicity)
+ IsPadding · HashTableServerLogDerivative
2. (1 - IsPadding)·(LookupTableClientLogDerivative·(🪒 - 🥦·LookInLo - 🥒·LookOutLo)·(🪒 - 🥦·LookInHi - 🥒·LookOutHi) - 2·🪒 + 🥦·(LookInLo + LookInHi) + 🥒·(LookOutLo + LookOutHi))
+ IsPadding·LookupTableClientLogDerivative

Consistency Constraints

1. IsPadding is 0 or 1.

Consistency Constraints as Polynomials

1. IsPadding·(1 - IsPadding)

Transition Constraints

1. If the current row is a padding row, then the next row is a padding row.
2. If the next row is not a padding row, then HashTableServerLogDerivative accumulates the next row with respect to challenges 🍒 and 🍓 and indeterminate 🧺. Else, HashTableServerLogDerivative remains unchanged.
3. If the next row is not a padding row, then LookupTableClientLogDerivative accumulates the next row with respect to challenges 🥦 and 🥒 and indeterminate 🪒. Else, LookupTableClientLogDerivative remains unchanged.

Transition Constraints as Polynomials

1. IsPadding·(1 - IsPadding')
2. (1 - IsPadding')·((HashTableServerLogDerivative' - HashTableServerLogDerivative)·(🧺 - 🍒·(2^8·LookInHi' + LookInLo') - 🍓·(2^8 · LookOutHi' + LookOutLo')) - LookupMultiplicity')
+ IsPadding'·(HashTableServerLogDerivative' - HashTableServerLogDerivative)
3. (1 - IsPadding')·((LookupTableClientLogDerivative' - LookupTableClientLogDerivative)·(🪒 - 🥦·LookInLo' - 🥒·LookOutLo')·(🪒 - 🥦·LookInHi' - 🥒·LookOutHi') - 2·🪒 + 🥦·(LookInLo' + LookInHi') + 🥒·(LookOutLo' + LookOutHi'))
+ IsPadding'·(LookupTableClientLogDerivative' - LookupTableClientLogDerivative)

Terminal Constraints

None.

Lookup Table

The Lookup Table helps arithmetizing the lookups necessary for the split-and-lookup S-box used in the Tip5 permutation. It works in tandem with the Cascade Table. In the language of the Tip5 paper, it is a “narrow lookup table.” This means it is always fully populated, independent of the actual number of lookups.

Correct creation of the Lookup Table is guaranteed through a public-facing Evaluation Argument: after sampling some challenge $X$, the verifier computes the terminal of the Evaluation Argument over the list of all the expected lookup values with respect to challenge $X$. The equality of this verifier-supplied terminal against the similarly computed, in-table part of the Evaluation Argument is checked by the Lookup Table's terminal constraint.

Base Columns

The Lookup Table has 4 base columns:

Extension Columns

The Lookup Table has 2 extension columns:

• CascadeTableServerLogDerivative, the (running sum of the) logarithmic derivative for the Lookup Argument with the Cascade Table. In every row, accumulates the summand LookupMultiplicity / Combo where Combo is the verifier-weighted combination of LookIn and LookOut.
• PublicEvaluationArgument, the running sum for the public evaluation argument of the Lookup Table. In every row, accumulates LookOut.